Introduction & Graphical Analysis
Analyzing Data: Solution to Problems
*Reference: Fundamentals of Physics: A Senior Course, Martindale et All, Heath Canada 1986; page 39
1. When a mass is placed on the free end of a board, the end is deflected downward.
The following table shows the downward deflection (d) corresponding to various lengths of board,
as measured in an experiment. Each deflection was produced by the same mass.
as measured in an experiment. Each deflection was produced by the same mass.
|
Length of board (I), (m)
|
1.0 | 2.0 | 3.0 | 4.0 | 5.0 |
| Downward deflection (d) , (cm) | 0.4 | 3.2 | 10.8 | 25.6 | 50.0 |
(a) Determine the relationship between d and I.
(b) Determine an equation relating d and I.
(c) Predict the deflection of the board when the length is 2.5 m, and when it is 6.0 m.
Solution:
a) plotting d vs. l yields a proportionality of the type d a ln
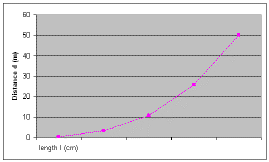
b) plotting d vs l3 gives us a linear relationship
Therefore, taking the slope of the line of d vs. l3 we obtain the proportionality constant k
Therefore, taking the slope of the line of d vs. l3 we obtain the proportionality constant k
where k = 0.40 cm/m3
Therefore the equation of the function is d = 0.40 l3
c) Now, for l = 2.5 m d = (0.40)(2.5)3 = 6.3 cm
and for l = 6.0 m d = (0.40)(6.0)3 = 86 cm
2. It can be shown that the kinetic energy Ek of a moving car is proportional to the square of its velocity
(i.e. Ek a v2 ). At 90 km/h, a certain car’s Ek is measured as 400 units.
(i.e. Ek a v2 ). At 90 km/h, a certain car’s Ek is measured as 400 units.
(a) What is the car’s Ek at 270 km/h?
(b) What is the car’s Ek at 45 km/h?
(c) What is the car’s velocity when its Ek is 16 units?
Solution
a) Ek a v2
Ek' = Ek[270/90]2
= 400 x 9
= 3.6 x 103 units
Ek' = Ek[270/90]2
= 400 x 9
= 3.6 x 103 units
b) Ek' = Ek[45/90]2
= 400 x 1/4
= 1.0 x 102 units
= 400 x 1/4
= 1.0 x 102 units
c) Ek a v2
Therefore v2 a Ek
And v a ÖEk
And v a ÖEk
v' = v[Ö(16/400)]
= (90 Km/h)(2/10)
= 18 Km/h
= 18 Km/h
3. The resistance (R) of 1000 m of nichrome wire is tabulated for various diameters (d).
From the following table, determine the mathematical equation relating electrical
Resistance and the diameter of a conductor
From the following table, determine the mathematical equation relating electrical
Resistance and the diameter of a conductor
| d | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 |
| R | 130 | 33 | 14 | 8.1 | 5.0 |
Solution:
Using similar techniques as in #1 we find that R a d-2
i.e. R a 1/d2 Therefore R = k / d2
Find k by taking logs or by calculating the slope of the line when you plot R vs. d-2
Then k = 1.3 X 10 -2 and
... the equation of the function is R = (1.3 X 10 -2 ) / d2
4. Measurements are made of the resistance (R) and the power consumption (P) of a tungsten filament lamp, with the following results.
| Power (P), in watts | 2.2 | 5.7 | 12.3 | 27.1 | 52.9 |
| Resistance (R), in ohms | 1.6 | 2.0 | 2.4 | 2.9 | 3.4 |
Show that the relationship between p and R is of the form P = a (R)n , and find the values of n and a. (Note that the resistance (R) is the "cold" resistance and may vary as the filament heats up.)
Solution:
P = aRn
log P = log a + nlog R
For P = 2.2, R = 1.6 and P =5.7, R = 2.0
Therefore... 0.3424 = loga + n(0.20412) ... (1)
And ........ 0.7558 = loga + n(0.3010) ... (2)
Subtract (1) from (2) to obtain:
0.4134 = 0.09688 (n)
Therefore n = 4.2
0.7558 = log a + 4.2(0.30101)
log a = -0.5085
a =0.31
Therefore, P = 0.31 R4.2


