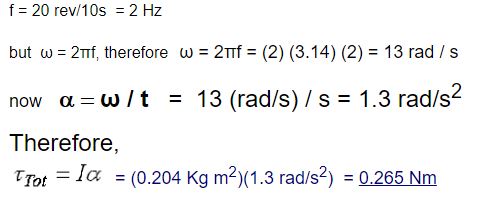Moments of Inertia
- Inertia is defineed as the property of an object to resist changes on motion.
- The ability of an object to continue to stay at rest or in its existing state of rest or uniform motion in a straight line.
- Unless that state is changed by an external, unbalanced force.
- Rotational Inertia measures the ability of an object to resist rotating about a fixed pint around a circular path.
- The moment of inertia is the ability of an object to resist a change in its angular acceleration.
- A torque is a force applied to an object, in a circular path, capable of alterning its moment of inertia or angular acceleration.
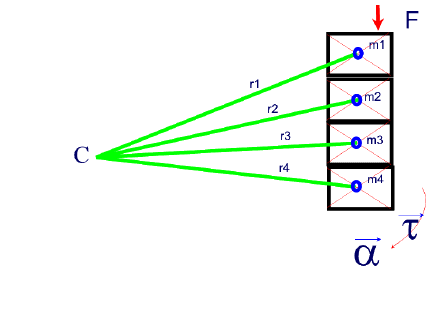
The total rotational torque taken at the center of gravity of a complex rotating object can be expressed as the sum of all torques acting on individual parts of the rotating object.
The illustration below is of a rectangular object rotating about a point C.
The object can be taken a s a whole or broken up into smaller masses, each rotating about slightly different radius from the center of rotation.
For the system above, for example,
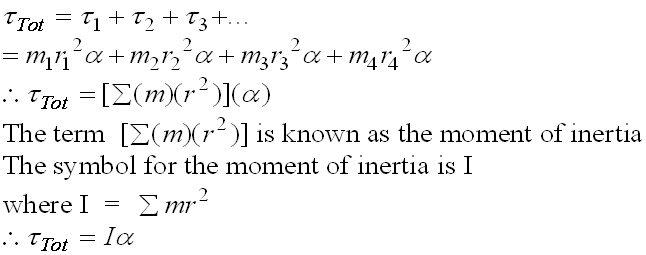
Example:
Two masses are suspended on a nylon thread of negligible mass as shown.
Find the moment of Inertia and the total torque of the system if it completes 20 revolutions in 10 s.
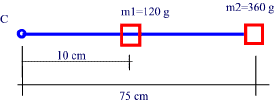
m1 = 0.12 Kg
m2 = 0.36 Kg
r1 = 0.1 m
r2 = 0.75 m
Solution:
a) Find the moment of inertia I
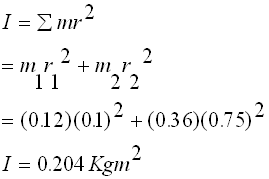
b) Find the total Torque
First find the angular acceleration a