Angular Acceleration Revisited
A particle, with mass m, is tied to a pivotal point by a massless string of length r. Friction is ignored.
The mass originally at rest, is given a sudden push under the action of a Force F, such that it starts to rotate about the fixed point C, and at a radius of rotation r.
The particle will experience a component of linear acceleleration a, but it will also experience a sudden change in motion along the circular path.
This means that it will also have "a circular or angular acceleration".
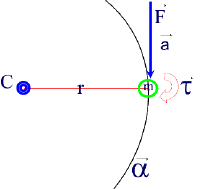
We will call this angular acceleration "alpha" ,a, (to distinguish it form the linear acceleration a) and we will define it mathematically as follows:
Consider a circle as shown below, as the particle moves along th arc s, spanning a number of radians from point A to point B. The radius of the circle is r.
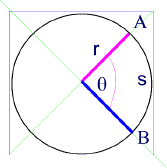
In a full circle, θ = 3600 , and 2Pr is the total circumference of the circle.
If we measure θ in radians, which is a linear measure, instead of degrees, then we can compare the two quantities by proportions and write:
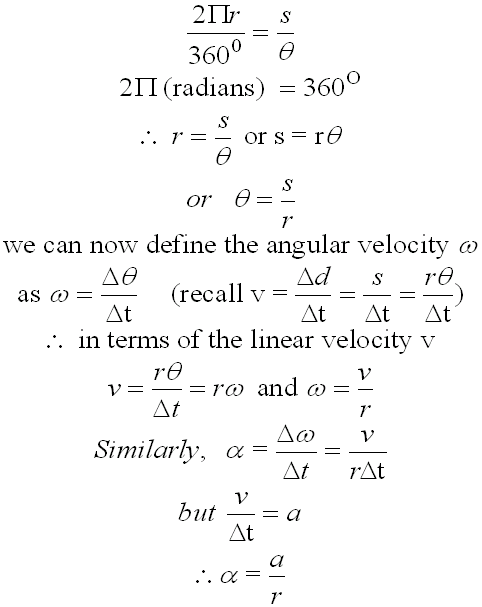
or simply .... a = a x r
Units of Angular Acceleration
Recall That :
F = m x a and from our definition of Torque, t = r x F ,
Let us multiply both sides of the equation by r, to obtain:
r x F = r x m x a ..... (1)
Now equation (1) can be rewritten in terms of a
where a = a x r (from our previous analysis)
r x F = r x m x a x r
or
r x F = m x a x r2
The above equation calculates the torque on a mass (m), hinged at point (C), at a distance (r) perpendicular to the force (F) which produces an angular acceleration (a) which is related to the linear (tangential) acceleration (a).
This torque is known as Rotational Torque, and mathematically can be written as:
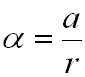
Let's now find the units of a, by using a a brief unit analysis
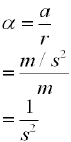
In linear quantities, the units 1/s2 may not make much sense. However, when we analyze these same units in a circular frame of reference we can get a better understanding of what their real significance is.
In the diagram, θ is the angle spanned by a particle as it moves from (A) to (B) along the circle with radius (r) and traces an arc (s), as we discussed at the beginning of this lesson.
The units of a are m/s2 and consequently, the actual units of a are radians/s2


