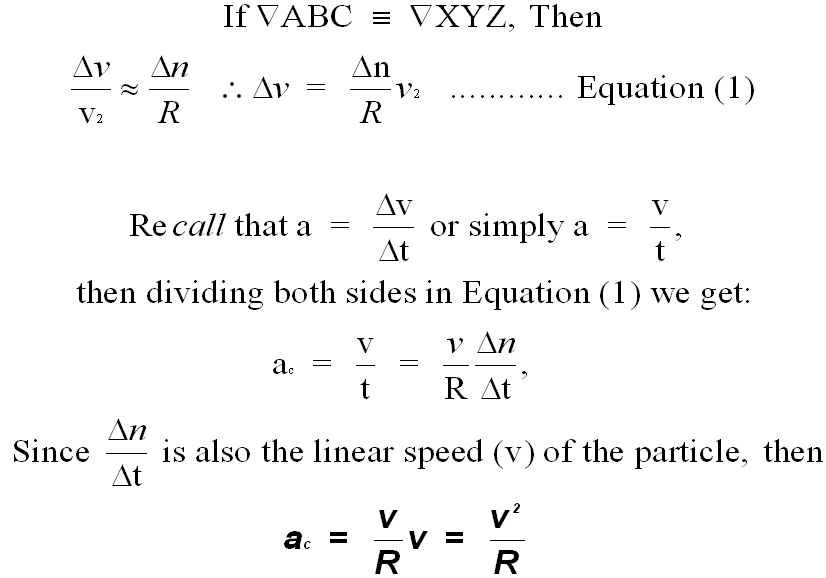Introduction to Cirular Motion
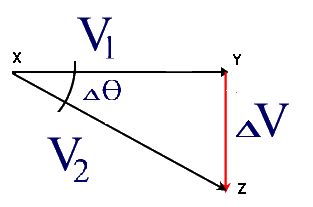
There is a constant component (Vav) along the path (C - the circumference of the circle) and tangential components (Vt1) and (Vt2) at right angles to the radius (R).
We can calculate the average velocity using the following equations
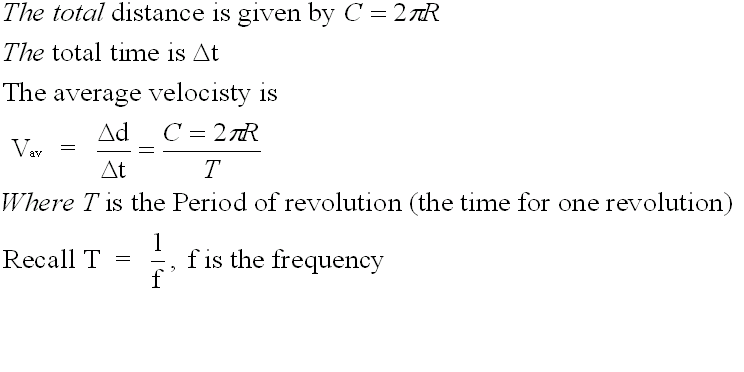
This is a special case of accelerated motion.
Note that the particle changes its direction along the path. This means that it will experience acceleration even if it is moving at constant speed.
Let's look at this acceleration mathematically

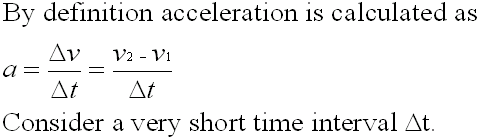
During this time, the particle will move from point A to point B.
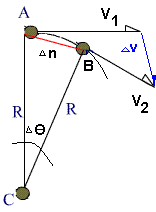
∆n is the small arc between the points A and B, and ∆θ is the small angle between A & B. If this angle is very small, we cay say that V1 and V2 will be almost be parallel to each other and ∆V can be considered to perpendicular to them.
If ∆V is perpendicular to either V1 or V2 , it will point towards the center.
If ∆V points towards the center, then the acceleration (a), will also point towards the center.
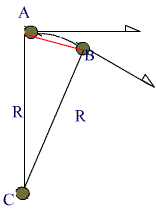
This acceleration is called Centripetal Acceleration (ac ).
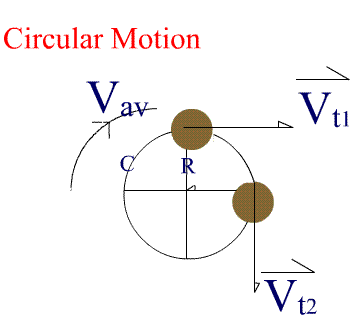
The magnitude of ac can be calculated using the two similar triangles above (ABC ~ XYZ) as follows: