Law of Universal Gravitation
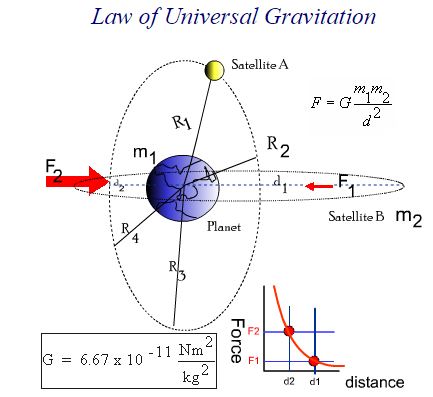
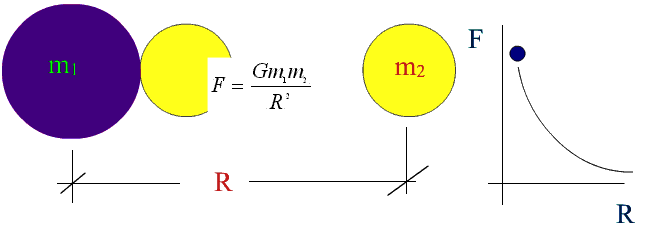
The force of attraction F between two objects with respective masses m1 and m2 separated by a center-to-center distance R, anywhere in the universe is described by Newton's Law of Universal Gravitation:
The two postulates of this law are:
- The force of attraction is directly proportional to the product of the objects' masses
- The force of attraction is inversely proportional to the distance (taken from their respective centers) squared
If we combine the above statements mathematically, we obtain the following relation:
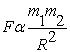
We translate the above statement into a definite equation by introducing a constant G
Therefore:
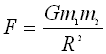
Which states that the force of attraction is inversely proportional to the distance (taken from their respective centers) squared
In the above Equation"
- F is the force of attraction between two masses m1 and m2 anywhere in the Universe, and
- and, G is the Universal Gravitational Constant: G = 6.67 X 10-11 Nm2 /Kg2
The value of g
Another way to calculate the acceleration due to gravity g is by using Newton's Law of Universal Gravitation
Recall that the Force of gravity around the surface of the Earth is calculated with the formula Fg = m x g
But we can also use Newton's Law of Universal Gravitation to obtain the same result. After all this equation is UNIVERSAL.
Therefore we can say that
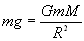
where m is the mass of any object at the surface of the Earth. M is the mass of the Earth G is the constant of Universal Gravitation (6.67 x 10-11 Nm2/kg2).
** Note that the mass m drops out from each side of the equation therefore the value of g on Earth can be calculated if we know the mass of the Earth and its radius R.
This fact should not surprise us after all we've always stated that the acceleration due to gravity on an object is independent of the object's mass
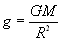
Exercise 1:
Use the information that the mass of the Earth is 5.98 x 1024 kg and that its radius is 6.38 x 103 km (6.38 x 106 m) to confirm that g on Earth is approximately 9.8 N/kg
Solution:
Using the formula above we have:

NOW... Do a unit analysis check on your own to verify that the answer is in N/kg -- good practice!
Exercise 2:
Given the following data use graphical techniques to confirm that Newton's Law of Universal Gravitation is an inverse square law.
.gif)
The center to center distance between the Moon and the Earth is the distance between the two celestial bodies plus their respective radii.
Moon -Earth System -- F1 = 2.05 x 1023 N
Sun -Earth System -- F2 = 3.53 x 1022 N
i.e.
- Moon -Earth System R1 = 1.74 x 106 m + 6.38 x 106 m + 3.84 x 10 6 m = 1.196 x 10 7 m
- Sun -Earth System R2 = 1.496 x 1011 m + 6.38 x 106 m + 6.96 x 10 8 m = 1.50 x 10 11 m
Find the forces using 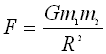
-
Compile the data in a chart and Plot the data
| System | Forces (N) |
Distances (R) (m) |
Distances-squared (R)2 , (m2) |
Product of Masses (kg2) |
| Earth-Moon | 2.05 x 1037 | 1.196 x 10 7 | 1.430 x 10 14 | 4.57 x 1047 |
| Earth-Sun | 3.53 x 1022 | 1.50 x 10 11 | 2.25 x 10 22 | 1.19 x 1055 |
Here is the same data and its analysis using spreadsheets
| System | Forces (N) | Distances (R) | Distances-squared (R)2 , (m2) | Product of Masses | Inverse Distances-squared (1/R)2 , (1/m2) |
| (m) | (kg2) | ||||
| Earth-Moon | 2.05E+37 | 1.20E+07 | 1.43E+14 | 4.57E+47 | 6.99E-15 |
| Earth-Sun | 3.53E+22 | 1.50E+11 | 2.25E+22 | 1.19E+55 | 4.44E-23 |
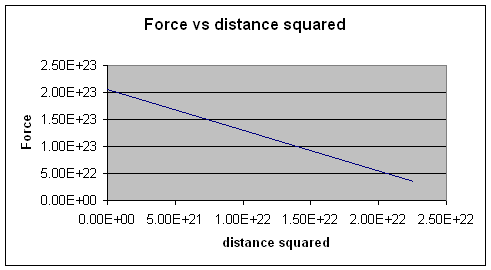
This shows the relationship F α 1/R2
To confirm plot F vs. 1/R2
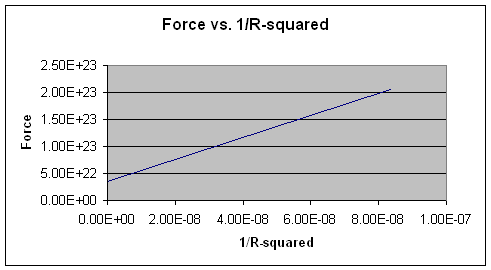
Note: F vs. 1/R2 gives us a linear relationship


