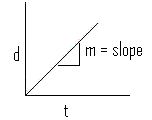Mathematical Development of Linear Motion Equations
Starting Point:
>>>The equation of motion (v2 = v1 + at) developed in the previous section is really a linear equation of the form: y = mx + b
Where::
m is the slope of the line, and b is the y-intercept
Using our kinematics symbols we can redefine the above relationship as follows:
y = mx + b is a liner function (a straight line) of v(t); "velocity as a function of time" in a distance-time graph
 recalling from previous knowledge
recalling from previous knowledge
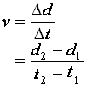
In a velocity-time graph, this becomes:
More specifically:
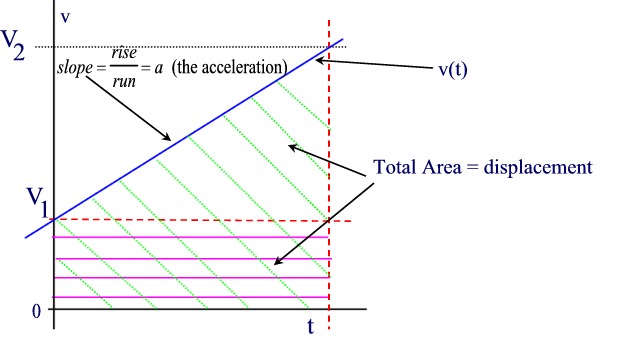

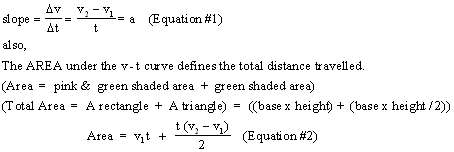
Using equations 1 and 2 we can obtain a
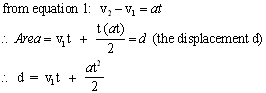
The above equation can also be written as d = v1t + 1/2 at2
Another useful equation can be derived as follows:
we start with our very first equation vav = d/t
Where vav is the average velocity, d is the total distance and t the total time.
We can also express the average velocity as vav = (v1 + v2)/2
Therefore,

Summary of the Five Essential Linear Motion Equations
| 1 |
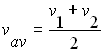 |
|
| 2 |
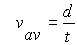 |
|
| 3 |
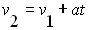 |
|
| 4 |
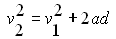 |
|
| 5 |
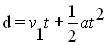 |