The Force of Friction
Look at the image below:
Here a block of wood with an iron mass (m) resting on top of it is being pulled along a surface with an applied force Fa.
If the applied force overcomes the force of Friction Ff, the object will move in the direction of the applied force Fa and the spring scale will show a reading in newtons of force.
![]() Note: The Force of Gravity on any object is pinting down perpedicular to the surface where the object is resting.
Note: The Force of Gravity on any object is pinting down perpedicular to the surface where the object is resting.
![]() Recall: The opposing force to the force of gravity is The Normal Force, FN. This force always points up and it is also perpendicular to the plane where the object is resting. The magnitude of the normal force is always the same as the force of gravity but in the opposite direction.
Recall: The opposing force to the force of gravity is The Normal Force, FN. This force always points up and it is also perpendicular to the plane where the object is resting. The magnitude of the normal force is always the same as the force of gravity but in the opposite direction.
When the applied force on an object is equal or less than the force of friction, the object will not move. If the applied force is slightly bigger than the force of friction, the object will move in the direction of the applied force. There are two types friction forces acting on the object.
- Static friction: before the object starts to move
- Kinetic friction: while the object is moving
- Static Friction is larger than Kinetic friction
Friction depends on several factors:
- The weight of the object i.e. the force of gravity ( Fg)
- Recall that Fg = m x g
- Friction also depends on the type of surface
- The presence or the absence of a lubricant
Three images of different surfaces seen under a microscope:
 |
 |
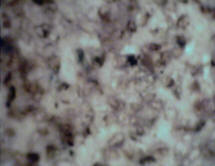 |
| Glass Surface Seen Under a Microscope | Sandpaper Surface Seen Under a Microscope | Sandpaper Surface with a few drops of oil Seen Under a Microscope |
Notice how relatively smooth a glass surface is when seen under a microscope compared to a piece of sand paper seen under a microscope. The imperfections (bumps and grooves) are much more pronounced in sandpaper; therefore friction is higher on a rough surface (sand paper vs. glass). Notice that adding a few drops of oil (a lubricant) to the sand paper makes the surface less rough.
The Coefficient of Friction
Surfaces can be classified using a degree of roughness called the Coefficient of static Friction.
The symbol for this coefficient is µs (µ is pronounced "mu")
The higher the Coefficient of friction, the rougher the surface, therefore the higher the friction force.
Mathematically we can express the force of static friction as
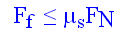
In the above equation
- Ff = Friction Force
-
µs = coefficient of static friction
- FN = Normal Force
![]() Recall that the normal force is equal in magnitude to the force of gravity i.e. FN = m x g
Recall that the normal force is equal in magnitude to the force of gravity i.e. FN = m x g
Therefore, in general we can say that :
Ff ≤ µsmg
![]() Note: The force of friction dose not depend on surface Area.
Note: The force of friction dose not depend on surface Area.
Therefore, to keep an object moving, one needs to keep applying an amount of force which is at least equal to the force of friction. This type of friction is known as moving or kinetic friction. The sumbol for the coefficient of moving friction is µk.
Generally speaking we can say that static friction is higher than kinetic (moving) friction because it takes more effort (force) to initially get an object moving than to keep it moving at constant speed. Symbolically this can be summarized as:
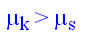
There are two possibilities to analyze the motion of an object on a surface that has friction:
-
If the object is moving at constant speed then the forces on the object are balanced and there is no acceleration
(V = constant, a = 0) -
If the object is moving at changing speed (a ≠ 0), that means that the forces are not balanced and the object experiences an acceleration.
We will look at this in more detail when we'll study Newton's Laws of Motion.
Example:
A 200 Kg crate of bricks ( made of wood) is pulled along a rubber floor. The coefficient of friction is 0.38. How much force is needed to move the crate?
Given: m = 200 Kg
g = 9.8 m / s2
µ = 0.35
Find: Ff
Solution: Ff = µ m g
= ( 0.35)(200 Kg)( 9.8 m / s2)
= 686 Kg m /(s2) = 686 N
.: The minimum force required to get the crate moving is 686 N



