Adding vectors using trigonometric methods
A) Pythagoras's Theorem & Trigonometry
![]() Review: Mathematical concepts in trigonometry
Review: Mathematical concepts in trigonometry
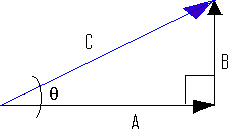
Recall Pythagoras's Theorem: C2 = A2 + B2
This theorem applies only to right angle triangles like the one below.
In other words, it can be used only when vector A is perpendicular to vector B
The three basic trigonometric identities that can be derived from a right angle triangle whose included angle is 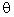 , are:
, are:
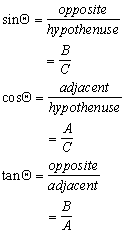
B) Sine and Cosine Laws Method
![]() For triangles that are NOT right-angle triangles we can use modified trigonometric laws known as the cosine and sine laws:
For triangles that are NOT right-angle triangles we can use modified trigonometric laws known as the cosine and sine laws:
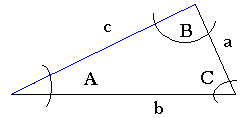
The triangle below is a generalized isosceles triangle where none of the sides are perpendicular to one another.
![]() Note that we use lower case letters to represent the sides of the triangle and upper case letters to represent the included angles.
Note that we use lower case letters to represent the sides of the triangle and upper case letters to represent the included angles.
![]() Memorize these two laws ... they will come in very handy
Memorize these two laws ... they will come in very handy
- The sine Law
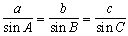
- The Cosine Law
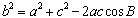
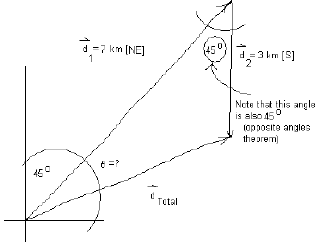
Example: What was the total displacement of a balloon that drifts for 7 km in a [NE] direction and then is pushed by a wind in a southerly direction for another 3 km.
![]() In case you forgot: [NE] is a direction half way between the y axis [N] and the x axis [E] ---> [N450E]
In case you forgot: [NE] is a direction half way between the y axis [N] and the x axis [E] ---> [N450E]
![]() Use the sine/cosine laws to solve this problem.
Use the sine/cosine laws to solve this problem.
Solution:
As usual we will start with a quick sketch
![]() Knowing the rules of angles here is also important. For example the Opposite Angles Theorem tells us that the angle between d1 and d2 (angle B) is also 450 - see diagram below:
Knowing the rules of angles here is also important. For example the Opposite Angles Theorem tells us that the angle between d1 and d2 (angle B) is also 450 - see diagram below:
![]() Step-by-step ...
Step-by-step ...
-
We first apply the cosine Law to find the magnitude of the resultant vector, dtotal
where:
b = dtotal (to be calculated)
a = 3 km [S];
c = 7 km [NE]
and
B = 450
therefore applying the cosine law
b2 = (3)2 + ( 7)2 - 2(3)(7)(cos(450))
and b2 = 28.3
and [ by taking the square root of b2]
b = 5.32 km ----> this is the magnitude of dtotal
2. Finding the direction of the resultant - Apply the Sine Law to find the value of the angle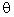
from the general equation 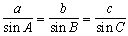
we can only use two of the terms for which we have information:
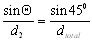
cross multiply, isolate, and solve for sin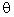
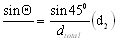
sin 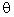 = 0.398
= 0.398
Now use the inverse of sin (sin-1) to find the angle in degrees
= invsin(0.398) = 23.500
3. Make a final statement indicating your findings
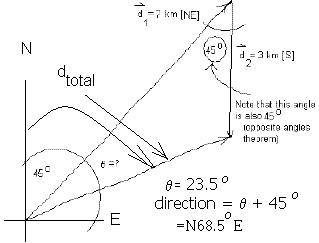
 the vector dtotal has direction (450 + 23.50) --- see diagram below
the vector dtotal has direction (450 + 23.50) --- see diagram below
 dtotal = 5.32 km [N68.50]
dtotal = 5.32 km [N68.50]