Work
The term "Work" in a scientific sense is very specific to a set of properties that apply to an object and is generally different that what we may impy with the word "work" in the everyday world.
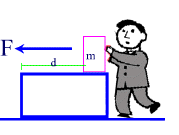
In Physics when we want to measure the work done on an object or by an oject we look at the energy used by the object or applied to the object in terms of two measurable quantities: the amount of force applied to an object and the distance that this force causes the object to move or change its state of motion, in the direction of the applied force.
Therefore if an object is pushed through a certain distance (d), using a force (F), the amount of work done in moving the object with mass m is given by the equation
WORK = Force X Parallel Distance
W = (F )(d)(cos q)
Where F is the Force doing the "pushing" and d is the distance the object moves. The distance and the force must be in the same direction.
In this equation, Force is measured in [N], and distance is measured in [m] and because the angle between the force and the distance is zero (the are parallel) then the cos q = 0.
![]() In general, the simplified equation for calculating work when the force and the distance are in the same direction is:
In general, the simplified equation for calculating work when the force and the distance are in the same direction is:
W = (F )(d)
Work-Energy Equivalence
![]() Note that work and energy are essentially the same thing. Energy is the work done on an object. And Work is the amount of energy required to alter the state of (motion) an object. This is known as the Work-Enetrgy Theorem.
Note that work and energy are essentially the same thing. Energy is the work done on an object. And Work is the amount of energy required to alter the state of (motion) an object. This is known as the Work-Enetrgy Theorem.
![]() In terms of units we can also show that WORK = Energy; when measured in Joules: 1 Joule = 1 Newton-meter or 1J = 1Nm
In terms of units we can also show that WORK = Energy; when measured in Joules: 1 Joule = 1 Newton-meter or 1J = 1Nm
Example 1:
A shopper pushes a cart with a force of 100 N, Through 50 m.
How much energy is she using up, and how much work is she doing on the cart?
Given: F = 100 NSolution:
d = 50 m
Find: W
W = F x d
= 100 N x 50 m = 5000 J
Therefore the shopper uses up 5000 N of Energy in pushing the cart.
At the same time, the work she is doing on the cart is also 5000N since Work = Energy.
If
Work = Force x distance
then
Energy = Force x distance.
Work done in LIFTING objects.
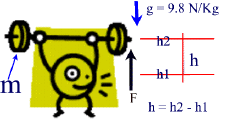
In the illustrations above, the mass m is being lifted from h1 to h2 against gravity. The change in height (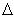 h) is calculated as [h2 - h1].
h) is calculated as [h2 - h1].
Now we can apply the equation for calculating work done.
W = F x d
= Fg x h
= m x g x h.
Therefore, When lifting a mass, the work done on it against gravity is:
W = m x g x h
This type of work is representative of the amount energy used in lifting the object. Because the object is being lifted against gravity, this energy is known as the Gravitational Potential Energy (Ep). It is a potential energy because, once lifted to a height above ground, the object has the potential of producing energy if released from that height.
Ep = m x g x 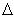 h
h
Example 2:
What is the work done by an elevator on 5 people (800 Kg) inside the elevator, if they all get off on the 4th. floor (12 m above the ground)?
Given:
m = 800 Kg,
g = 9.8 N/Kg,
h = 12 m
Find: W
Solution:
W = m x g x h
= 800 Kg x 9.8 N/Kg x 12 m
= 94080 Nm
= 94 080 J
Therefore the elevator does 94 080 J (or 94 KJ) to lift the passengers


