The Hexadecimal Code
Think of the hexadecimal code as an extended binary code
Binary code is made up of sets of one bit (either 0 or 1) – LED ON or LED OFF
Hexadecimal code is made up of sets of four bits.
In general, computers use Assembly Language to carry out instructions.
Assembly language is virtually written entirely using hexadecimal code.
We can convert each set of four binary bits into a single hexadecimal bit.
This allows for more information to be stored and retrieved more efficiently.
Changing from binary [BASE 2] to hexadecimal [BASE 16] is called a four-bit conversion.
Comparing the number systems
Decimal
- ten possible digits (0 to 9)
Binary
- two possible digits (0 and 1)
Hexadecimal
- sixteen possible digits (0 to 9 + A to F)
Converting BASE 2 to BASE 16
- Divide binary numbers in groups of 4
- Assign the hexadecimal value to each group
- If a group does not have 4 digits add zeros in front of it
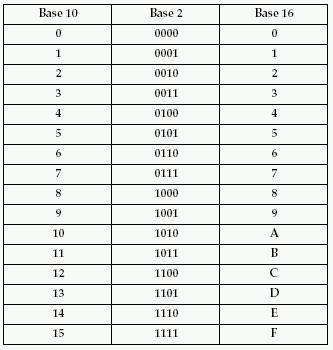
Example 1: convert 1000111 into hexadecimal
- First group = 0111
-
Second group = 0100
(noticed we added a 0 in front of the one)
Group 1
- 0111 = 7 (from the chart)
Group 2
- 0100 = 4
Therefore 1000111 = 47
Example 2: convert 101110101101 into hexadecimal
1011 1010 1101
- First group = 1101
- Second group = 1010
- Third group = 1011
Group 1
- 0111 = “D” (from the chart)
Group 2
- 1010 = “A”
Group 3
- 1010 = “B”
Therefore:
101110101101 = “BAD” in hexadecimal code


