Emission Spectra
When an object is heated to very high temperatures atoms become excited and give off energy in the form of radiation. At high temperatures visible light is emitted.
We see it as white light. Using a spectroscope, a devise that breaks light into its component colours, it is observed that white light produces a CONTINUOUS SPECTRUM. It contains all the colours in an unbroken line.
The visible part of the spectrum may be further subdivided according to color, with red at the long wavelength end and violet at the short wavelength end, as illustrated (schematically) in the following figure.
The visible spectrum: RED - ORANGE-YELLOW-GREEN-BLUE-VIOLET

Not all emitters of light radiate at all wavelengths. Some radiate a few colours and are observed as a series of individual lines.

The Helium spectrum

The Nitrogen spectrum
These spectra are called ATOMIC SPECTRA or EMISSION SPECTRA.
On an atomic level, when gases or vapors of a substance are heated in an electric arc or a Bunsen burner flame, the atoms absorb energy.
The electrons will jump from their normal positions (the ground state) to outer levels, which are higher energy states.
The atoms are then said to be in an excited state. When an electron falls back to a lower level, after being excited, it emits a definite amount of energy, which is given off as a quantum of light. Passing the light emitted by an element through a prism gives the atomic emission spectrum of the element.
Each line in this spectrum corresponds to a characteristic frequency, wavelength, and energy.
The emission spectrum of each element is unique, which makes it useful for identification. See the emission spectrum of helium and nitrogen above.
In 1884, Johann Balmer energized atoms of hydrogen gas and examined the light produced with a spectroscope. He found 4 prominent colored lines, but was unable to explain their origin.
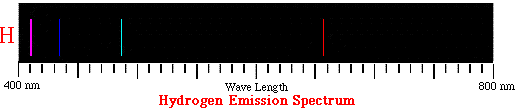
Balmer examined the four visible lines in the spectrum of the hydrogen atom; their wavelengths are 410 nm, 434 nm, 486 nm, and 656 nm.
He played around with these numbers and eventually figured out that all four wavelengths (symbolized by the Greek letter lambda) fit into the equation. He showed that the wavelengths of light for the visible region of the emission spectrum of hydrogen could be calculated using the Rydberg equation:
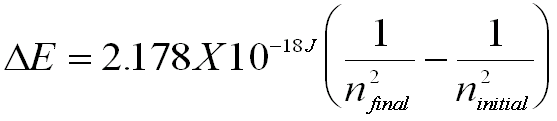
with n = 1, 2, 3, ... and R = 2.178x 10-18 J (called the Rydberg constant). The number n is just an integer; the above formula gives the longest wavelength, 656 nm, when n=3, and gives each of the shorter wavelengths as n increases up to 6.
The energy level transitions for the hydrogen atom with a final level of n = 2 is known as the Balmer series and has the wavelengths given in the table below. Also refer to the diagram below referring tothe various energy levels of the Hydrogen atom.
|
Color
|
Wavelength
|
|
red
|
6.563 x 10-7 m
|
|
blue-green
|
4.861 x 10-7 m
|
|
blue
|
4.340 x 10-7 m
|
|
violet
|
4.102 x 10-7 m
|
From Balmer's equation, it is evident when n gets bigger, the lines should start getting closer together.
As n gets larger, 1 over n squared gets smaller, so there's less and less difference between the consecutive lines.
You can see that the series has a limit-- that is, as n gets larger and larger, the wavelength gets closer and closer to one particular value. If n is infinity, then 1 over n squared is 0, and if you work out the numbers, you'll find that the wavelength is about 365 nm.
That's just what experimentalists saw; around 365 nm, the lines became too close together to distinguish.
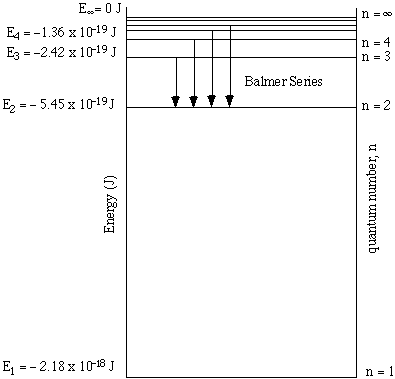
Energy levels in the Hydrogen atom and electronic transitions of the Balmer series

Energy levels in the Hydrogen atom and electronic transitions of the Balmer series
It was not until 1913 that Neils Bohr satisfactorily explained the origin of the spectral lines.
Proposals made by Max Planck in 1901 and then by Albert Einstein a few years later, provided the clues Bohr needed.
The Bohr model is a planetary model of the atom that explains things like line spectra. Neils Bohr proposed the following:
- He began with the assumption that electrons were orbiting the nucleus, much like the earth orbits the sun.
- From classical physics, a charge traveling in a circular path should lose energy by emitting electromagnetic radiation
- If the "orbiting" electron loses energy, it should end up spiraling into the nucleus (which it does not). Therefore, classical physical laws either don't apply or are inadequate to explain the inner workings of the atom
- He borrowed the idea of quantized energy from Planck
- He proposed that only orbits of certain radii, corresponding to defined energies, are "permitted"
-
An electron orbiting in one of these "allowed" orbits:
- Has a defined energy state
- Will not radiate energy
- Will not spiral into the nucleus
If the orbits of the electron are restricted, the energies that the electron can possess are likewise restricted and are defined by the equation:

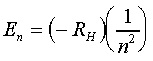
Where RH is a constant called the Rydberg constant and has the value 2.18 x 10-18 J
'n' is an integer, called the principle quantum number and corresponds to the different allowed orbits for the electron.
Thus, an electron in the first allowed orbit (closest to the nucleus) has n=1, an electron in the next allowed orbit further from the nuclei has n=2, and so on.
Thus, the relative energies of these allowed orbits for the electrons can be diagrammed as follows:
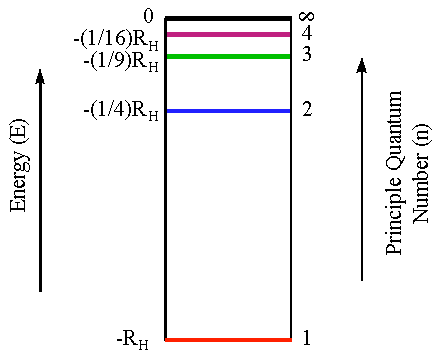
All the relative energies are negative
- The lower the energy, the more stable the atom
- The lowest energy state (n=1) is called the ground state of the atom
- When an electron is in a higher (less negative) energy orbit (i.e. n=2 or higher) the atom is said to be in an excited state
-
As n becomes larger, we reach a point at which the electron is completely separated from the nucleus
- E = (-2.18 x 10-18 J)(1/infinity) = 0
- Thus, the state in which the electron is separated from the nucleus is the reference or zero energy state (actually higher in energy than other states)
Bohr also assumed that the electron can change from one allowed orbit to another
- Energy must be absorbed for an electron to move to a higher state (one with a higher n value)
- Energy is emitted when the electron moves to an orbit of lower energy (one with a lower n value)
- The overall change in energy associated with "orbit jumping" is the difference in energy levels between the ending (final) and initial orbits:
∆E = Ef - Ei
Substituting in for the previously defined energy equation:
En = (–RH) (1/n2)
∆E = (-RH/ n2f) – (-RH/ n2i) = (-RH)(1/ n2f – 1/ n2i) = RH(1/ n2i – 1/ n2f)
When an electron "falls" from a higher orbit to a lower one the energy difference is a defined amount and results in emitted electromagnetic radiation of a defined energy, ∆E
- Planck had deduced that the energy of the photons comprising EM radiation is a function of its frequency (E = hυ)
- Therefore, if the emitted radiation from a falling electron had a defined energy, then it must have a correspondingly defined frequency
∆E = RH(1/n2i –1/n2f) = hυ
- ∆E is positive when nf is greater than ni, this occurs when energy is absorbed and an electron moves up to a higher energy level (i.e. orbit).
- When ∆E is negative, radiant energy is emitted and an electron has fallen down to a lower energy state
Revisiting Balmer's equation:
In 1885 a Swiss school teacher figured out that the frequencies of the light corresponding to these wavelengths fit a relatively simple mathematical formula:
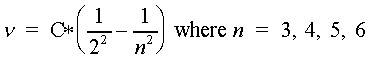
where C = 3.29 x 1015 s-1 ( Note: This is not the same 'c' used for the speed of light).
Since energy lost by the electrons is energy "gained" by the emitted EM energy, the EM energy from Bohr's equation would be:
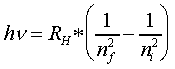
Balmer's constant 'C' = (RH/h) (Rydberg constant divided by Planck's constant), and nf = 2.
The only emitted energies which fall in the visible spectrum are from those electrons which fell down to the second quantum orbital. Those which fell down to the first orbital have a higher energy (frequency) than can be seen in the visible spectrum.
Sample Problem:
Calculate the wavelength of light that corresponds to the transition of the electron from the n=4 to the n=2 state of the hydrogen atom. Is the light absorbed or emitted by the atom?
Since the electron is "falling" from level 4 down to level 2, energy will be given up and manifested as emitted electromagnetic radiation:
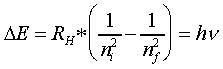
∆E = (2.18 x 10-18 J)((1/16)-(1/4)) = -4.09 x 10-19 J (light is emitted)
4.09 x 10-19 J = (6.63 x 10-34 Js) * (n)
6.17 x 1014 s-1 = n
l = (3.00 x 108 m s-1)/ (6.17 x 1014 s-1) = 4.87 x 10-7m = 487 nm
Bohr's model of the atom was important because it introduced quantized energy states for the electrons.
However, as a model it was only useful for predicting the behavior of atoms with a single electron (H, He+, and Li2+ ions).
Thus, a different model of the atom eventually replaced Bohr's model.


