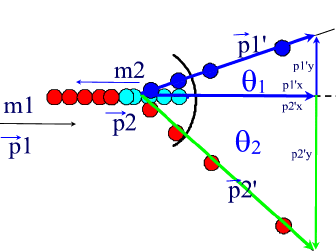
Collisions in Two Dimensions
Momentum is a vector quantity and as such direction is important in any collision analysis.
Elastic Collisions (during which both Kinetic Energy and Momentum are conserved) can be of two types:
-
HEAD-ON
-
NON HEAD-ON
Non Head-on collisions are usually more common.
In sports and games such as billiard and bocce ball these types of collisions are more frequent.
Non head-on collisions also occur in traffic accidents, nuclear experiments and so on.
The animations below describe the interaction of two billiard balls and the relative momentum equations/vector graphics:
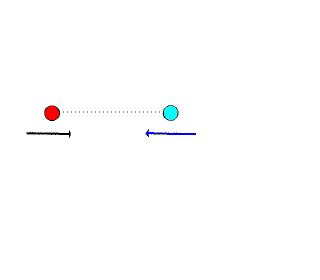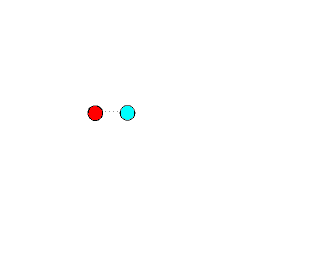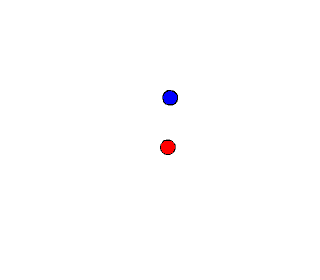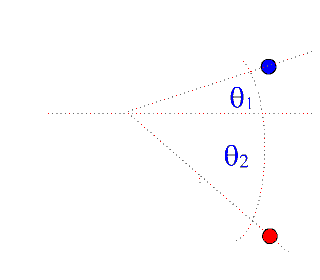
Example:
During a billiard game, one ball hits a second identical ball at rest, with a speed of 8.2 m/s.
One of the balls goes off at an angle of 600 At what angle will the second ball go off and what will the velocities of the two balls be after the collision?
Solution:
This is an elastic collision. Therefore, both kinetic energy and momentum are conserved.
Part 1. Conservation of Kinetic Energy.
Given: m1 = m2 (balls are identical); v2 = 0 m/s (at rest); v1 = 8.2 m/s; θ1 = 600
Therefore the equation for the conservation of kinetic energy
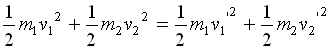
becomes:
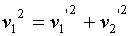....... Equation (1)
Part 2. Conservation of Momentum.
The equations for the conservation of Momentum
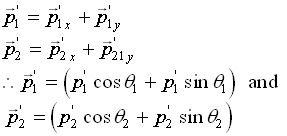
The above equation, for X-direction can be written as
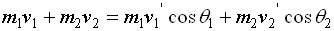
and in the y-direction, we can write it s:
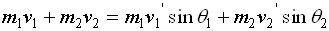
applying the given conditions:
- v2 = 0 m/s,
- m1 = m2,
- θ1 = 600
- v1 = 8.2 m/s
and the fact that there is no initial movement in the y-direction,
we obtain the following two equations:
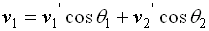......... Equation (2)
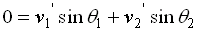........... Equation (3)
