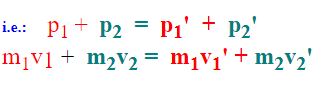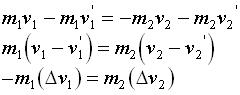Collisions and Conservation of Momentum
There are two types of collisions:
-
Elastic
-
Inelastic
Inelastic Collisions occur when only momentum is conserved. Some kinetic energy is transformed into heat or other forms of energy. The maximum amount of energy lost in a collision occurs when two bodies collide and subsequently stick together. This is an example of an inelastic collision.
Elastic collisions occur when both Kinetic Energy and Momentum are conserved.
Consider an object m1 with velocity v1 colliding with a second object m2 with velocity v2 traveling in the opposite direction of m1.
After the collision the two objects will rebound and have velocities v1' and v2' .
This type of collision is called an elastic collision.
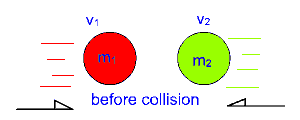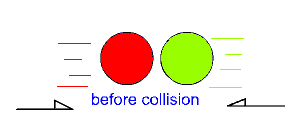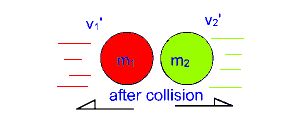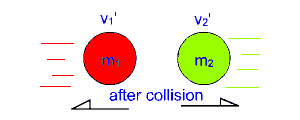
Where:
- m1 is the mass of the first object, m2 is the mass of the second object
- v1 is the initial velocity of the first object, v2 is the initial velocity of the second object
- v1' is the final velocity of the first object, v2' is the final velocity of the second object
Before the collision the first object will have momentum p1 = m1v1 and the second object will have momentum p2 = m2v2.
After the collision the first object will have momentum p1' = m1v1' and the second object will have momentum p2' = m2v2'.
The Law of Conservation of Momentum tells us that the momentum of a closed system before a collision is equal to the momentum after the collision.
rearranging and collecting "like" terms on both sides of the equal sign we can rexpress the above as:
This simple equation is a a re-statement of Newton's Third Law of Motion: "For every Action there exists an equal but opposite reaction".
It can now be rewritten so that it is finally expressed in terms of forces:
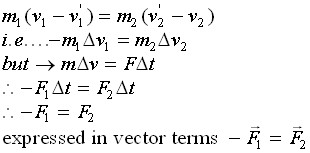
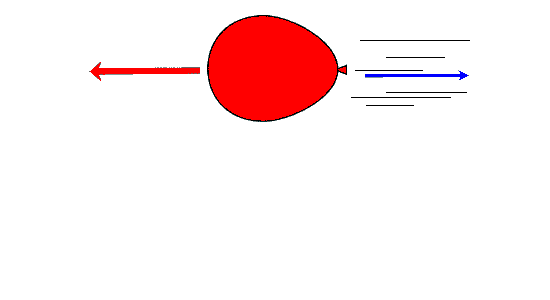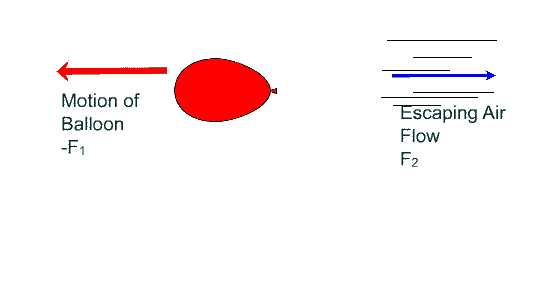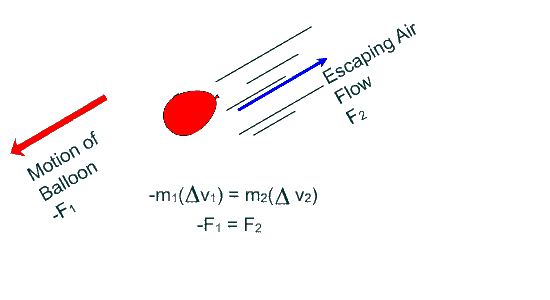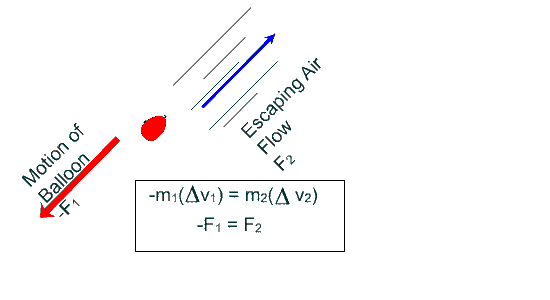
Cosider a practical application:
the air in an inflated balloon is allowed to suddenly escape as the ballon is released:
In the following illustration the balloon moves in the opposite direction of the air flow.
Conservation of Momentum example:
A proton (mass = 1.67 X 10-27 Kg ) with velocity of 1 X 107 m/s collides with a motionless He (Helium) nucleus.
The proton bounces back at 6 X 106 m/s.
The He nucleus moves forward with a velocity of 4 X 106 m/s .
The collision lasts 1 s.
Calculate:
a) the mass of the helium nucleus
b) The force that acts during the collision
Solution:
vHe = 0 m/s vHe' = 4 X 106 m/s
mp = 1.67 X 10-27 Kg
vp = 1 X 107 m/s (before collision)
vp' = -6 X 106 m/s (AFTER collision)
a) Find: mHe = ?
mpvp + mHevHe = mpvp' + mHevHe' BUT mHevHe = 0
(mpvp - mpvp' ) / vHe' = mHe = 7 x 10-27 Kg
b) F∆t = m∆v
... F = (m∆v) / ∆t
... Where ∆t = 1 s
Now,
F = (mHevHe' - mHevHe) / ∆t
= 2.8 X 10-20 N