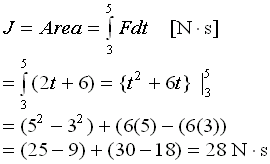Impulse & Momentum
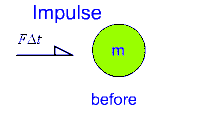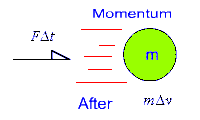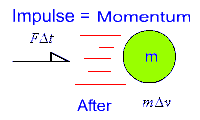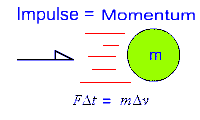
In "real-life" it is often easier or more convenient to analyze the dynamics of a moving object using energy and momentum considerations rather than force-acceleration methods.
Momentum is related to force:
From Newton's Second Law
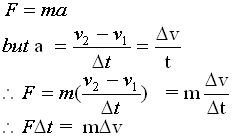
- The left side of the above equation is known as the Impulse (symbol "J").
- The impulse of an object can be described as the force (that caused the object to change its state of motion) acting on the object for a given period of time.
- Note that impulse is a vector quantity.
Thus one must also take into account its direction as well as its magnitude.
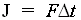 The unit of j is the N.s
The unit of j is the N.s
- The right side of the equation is known as the change in momentum.
- The change in momentum of an object is given the symbol ∆p.
- Momentum is also a vector quantity and can be defined as the mass-velocity product.
- Momentum is sometimes used as an indicator for the inertia of an object.
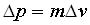 The unit of ∆p is the Kg.m/s
The unit of ∆p is the Kg.m/s
In general, for an object in motion, we can say the the Impulse is equal to the Change in Momentum.
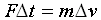
j = ∆p
Example:
A 10 Kg bowling ball moves in a straight line at a constant speed of 10 m/s. A constant force acts on the ball for 4.0 s giving it a velocity of -2.0 m/s. Calculate:
a) The Impulse acting on the bowling ball
b) The magnitude and direction of the Force
c) The momentum before and after the force acts on the ball
Solution:
a) j = m(∆v) = m(v2 - v1) = 10 Kg (- 2 m/s - 10 m/s) = -120 N.s (opposite to initial velocity)
b) F(∆t) = m(∆v)
= j
F = j / ∆t = -120 N.s / 4.0 s = - 30 N (opposite to initial motion of ball)
c) Initial momentum j1 = m v1 = (10 Kg)(10.0 m/s) = 100 Kg m /s
Final momentum j2 = m v2 = (10 Kg)(-2.0 m/s) = -20 Kg m /s
Momentum - Graphical Analysis
Sometimes the action of a force is expressed as a function of time. This is true when there is changing conditions such as sudden change sin magnitude or of direction.
In this case momentum is evaluated by considering the area under the F- ∆t graph.
Example:
The force F on a 1 Kg mass is described by the function F(t) = 2t + 6 [N]. What is the resulting impulse between 3.0 s and 5.0 s.
Solution 1.
a) Build a table of values
| F (N) | 6 | 8 | 10 | 12 | 14 | 16 | 18 |
| t (s) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
b) Graph F(t) = 2t + 6
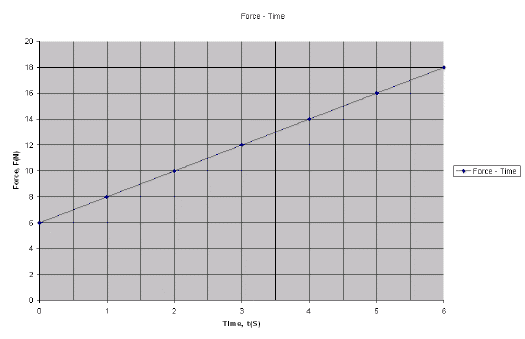
c) Calculate the area under the function from 3s to 5s
Area = j = F ∆t = (16 + 12)(2) / 2 = 28 Ns
Alternative Solution - Integral Calculus
The area under a function can be also calculated by integrating the function.
In this case: