Center of Mass
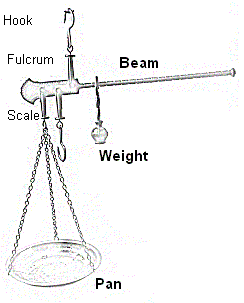
The two pictures shown below ae of the same scale in different static equilibria situations.

In the first picture the "weight" is moved to the right hand side of the beam. As you can see, the components of the vertical forces are quite different than in the second scale (even though ΣFy= 0 and ΣFx= 0 -- conditions for static equilibrium are satisfied). If we wanted to bring the beam back to the "zero" point on this scale we would have to add more masses to the pan.
In the second scale the "weight" is moved closer to the fulcrum. This allows the beam to assume a horizontal position.
In the second scale the "weight" is placed at the center of mass of the beam so that the force in the vertical direction (FN) is balanced against the force of gravity.
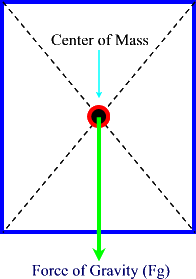
The above example illustrates that for any given object, the force of gravity can be considered to act upon a single point.
This point is called the center of mass and sometimes it is also referred to as the center of gravity.
The force of gravity, as we know, acts on all parts of an object.
In Physics we place the force of gravity at the center of mass of the object in question.
This helps us to draw free body diagrams and analyze the motion of the object and its statric dynamic properties.
Usually, regularly shaped objects and regular geometric figures have their center of mass placed at the geometric center.
For other irregular objects we can use the concepts of Torque and Statics to find the location of the center of mass.