Circular Motion - Problems & Solutions
1. A child playing on a beach fills a 500 mL bucket with water, attaches a 1.0 m string to it and starts to whirl it in a horizontal circle 1.2 m above his head.
A lifeguard standing 5.0 m away, counts how many times the child spins the bucket.
After exactly 30 s the child completed 15 revolutions (spins) of the bucket. The lifeguard, starts to walk towards the child to make him stop as some people on the beach are getting annoyed.
The child suddenly stops spinning the bucket, lets go of the string (and bucket) and takes off..
a) Explain what happens.
c) Use your knowledge of Physics to give quantitative analysis of the events that unfold.
Hints:
- Free Body Diagram
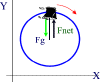
- Equations
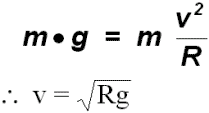
2. The wheel of a bicycle has a radius of 34 cm. The bicycle travels at 20 km/h. How many revolutions does the wheel on the bicycle make?
Solution:
Given: r = 0.34 m
d = 2.0 km = 2.0 x 103 m
Find q
3. A centrifuge spins a set of test tubes starting from rest and slowly accelerates to 10 000 RPM in 7 minutes. How many revolutions did it take the centrifuge to reach this speed?
Solution:
Given: Dt = 420 s = 7.0 min
f = 10 000 RPM
w1 = 0
Find q
First find the average angular velocity wav
Next find the total angular distance qtot
4. Tarzan (85 kg mass) swings from vine to vine. His arms generate a Tension force of 1500 N on a typical vine which is 4.0 m long. What maximum speed will he achieve on a typical swing at its lowest point?
Free Body Diagram
At the bottom of the swing T - Fg = Fc
Given
T = 1 500 N
m = 85 kg
g = 9.8 N/kg
r = 4.0 m
Rearrange the above equation and solve for v
5. A 1200 kg car enters a banked section of a curved highway at a speed of 70 km/h. The curve has a radius of 50 m and the road is banked at 160. How much friction force will be required to keep the car from skidding?
Solution:
Given
v = 70 km/h = 19.4 m/s
g = 8.8 N/kg
r = 50.0 m
q = 160
>>>>> Draw a Free Body Diagram
Equations:
Horizontal direction: Fc = Ffcosq + FNsinq
Vertical Direction: FNcosq = Fg + Ffsinq
Substitute the given data and the fact that
Solve for Ff:
Ff = 5 500 N [down the banked road]


