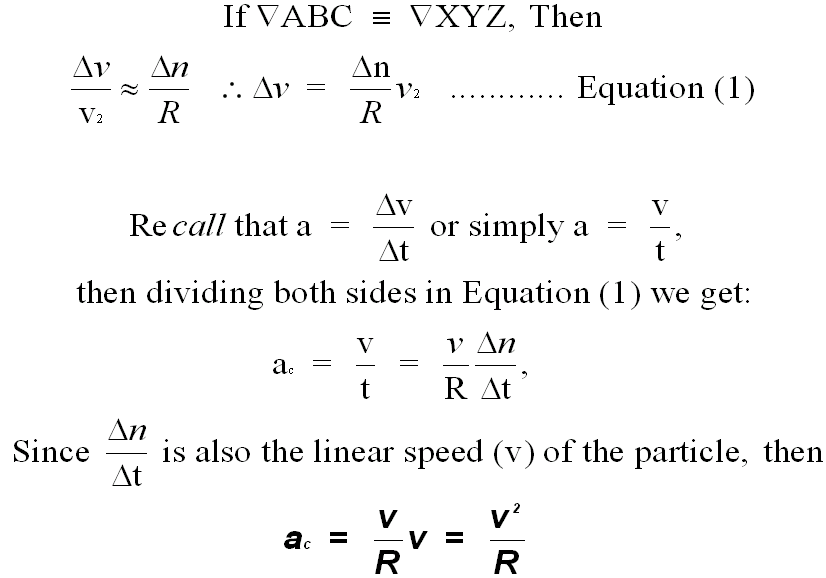Physics 12-U

Parent Category: Physics 12-U

Introduction to Cirular Motion

Examine the above diagram:
Here a small object (or a particle of very small mass) is revolving in a circular path.  Note that it has has two components of velocity.

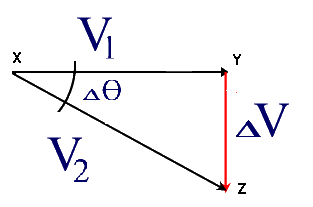
There is a constant component (Vav) along the path (C - the circumference of the circle) and tangential components (Vt1)  and (Vt2) at right angles to the radius (R).

We can calculate the average velocity using the following equations

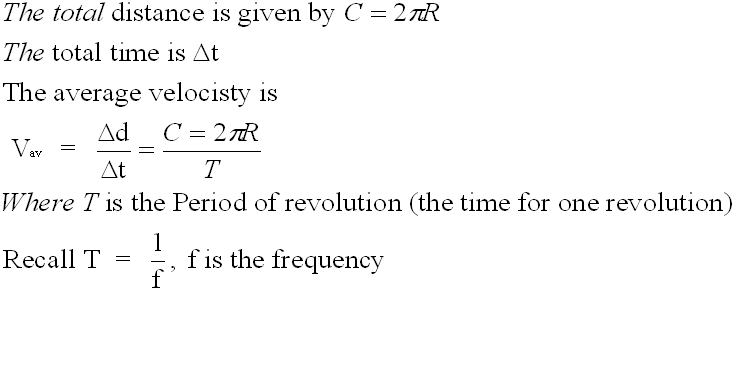
This is a special case of accelerated motion.

Note that  the particle changes its direction along the path.  This means that it will experience acceleration even if it is moving at constant speed.

Let's look at this acceleration mathematically

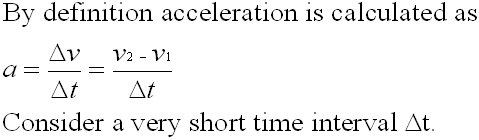
During this time, the particle will move from point A to point B.
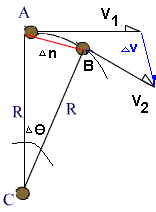
∆n is the small arc between the points A and B, and ∆θ is the small angle  between A & B.  If this angle is very small, we cay say that V1 and V2  will be almost be parallel to each other and ∆V can be considered to perpendicular to them.

  If ∆V is perpendicular to either V1 or V2 ,  it will point towards the center.

 

If ∆V points towards the center, then the acceleration (a), will also point towards the center.  

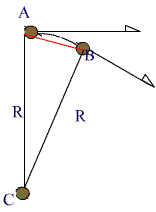
This acceleration is called Centripetal Acceleration (ac ). 

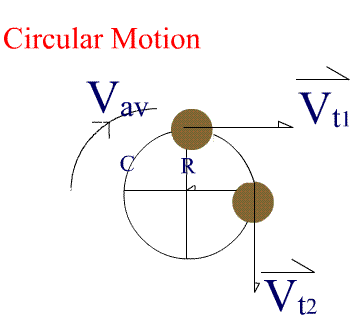
The magnitude of  ac  can be calculated using the two similar triangles above  (ABC ~ XYZ) as follows: