Acceleration due to Gravity
Free Fall:
Briefly look at --> Review of "Acceleration due to Gravity" from Grade 11 Physics
Free Fall is defined as the state of vertical (downward) motion of an object occurring solely under the influence of gravity. The object will have no strings attached to it, no self propelling engines or fuel sources, no other machines, pulleys, etc. governing its descend.
A rock falling off a cliff is said to be in "free fall"
Gravitational Field Intensity
What causes "free fall"? Think of the Earth as a giant magnet that attracts everything towards its center.
This attraction is due to a "force field" that surrounds the Earth; much like the area surrounding a magnet. This type of force is known in Physics as the "Force-at-a-distance" effect. Unlike, for example, the force experienced by a soccer ball when you kick it - here you have to apply an actual "contact force to make the ball change its state of motion (also see Newton's Laws of Motion).
The force field due to gravity surrounding a planet (gravitational field intensity) is pretty well constant around the surface of the planet. Its strength depends on several factors:
- The size of the planet
- The density of the core of the planet
- The make up of the core of the planet
The magnitude (or value, or size) of the gravitational field intensity on earth is a constant called g. We will discover the value of this constant with a simple experiment.
The Value of "g" on Earth - A simple discovery
Let us recall two basic terms before we start:
-
mass - a scalar quantity - the amount of substance in an object - measured with a scale or balance in kg
-
Force of gravity - a vector quantity - the weight of an object or the force of attraction with which an object falls down to Earth - measured with a spring scale in N (Newtons)
Step 1. Let's measure the mass (m) of two apples with a balance and then their respective forces of gravity (Fg) with a spring scale
| Object | Mass | Force of Gravity | |
| grams | kilograms | Newtons | |
| Red Apple |
 |
0.256 kg |
 2.50 N 2.50 N |
| Green Apple |
 |
0.136 kg |
 1.40 N 1.40 N |
Step 2. We organize the data in a table
| object | mass ( kg) | Force of Gravity (N) |
| m | Fg | |
| red apple | 0.256 | 2.50 |
| green apple | 0.136 | 1.40 |
Step 3. We plot the data collected in the table above
(recall that mass (m) should be on the x-axis because it is the independent variable) and we draw the line of best fit.

Step 4. We calculate the slope of the line - Note that m vs. Fg yields a linear relationship
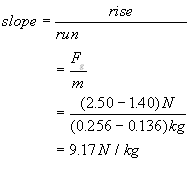
From this graph, which is of the form y = kx, (where k is the slope of the line) we can deduct a simple equation that relates the force of gravity Fg with the mass m.
This simple equation is:
Fg = k m
k is the slope of the line and is a constant value of 9.17 N/kg
Step 5. We test this value against a controlled, known value for accuracy.
|
|
|
|
Here we have a 200 g mass or 0.200 kg |
Here we have the corresponding weight or force of gravity of almost 2.0 N |
Conclusions:
-
Any object (regardless of its mass) experience a force of gravity nearly 10 times the value of its mass.
-
This is due to a constant gravitational field intensity (or acceleration due to gravity) around the surface of the Earth.
-
The accepted (tested) value of this constant is 9.81 N/kg or 9.81 m/s2.
Another name for the "gravitational field intensity" is "acceleration due to gravity".
They both have the same value 9.8 N/kg or 9.8 m/s2 respectively.
This value was first calculated by Galileo Galilei using a series of extremely simple but ingenious experiments.
Galileo noticed that objects (pendulums, and cannon balls) rolled down inclined planes at the same rate regardless of their mass but would speed up if the angle of the incline increased (that is of course if we ignore air resistance and keep all other things controlled -- like the frictional force).
The steeper the slope of the incline, the higher the acceleration of the object down the ramp.
If you want to read more about Galileo's life and classic experiments go to www.pbs.org/wgbh/nova/galileo.
The acceleration of an object down an inclined plane (a) is equal to the value of the acceleration due to gravity (g) diluted by a factor corresponding to the sine of the angle of the incline with respect to the horizontal (sinq).
a = g x sinq
Facts and Misconceptions about gravity
- All objects fall at the same rate of change of downward speed or acceleration.
- The mass of an object does not influence the acceleration of an object in free fall.
- The surface area of an object will influence the acceleration of an object in free fall because of the added air resistance factor
- In the absence of air, close to the Earth's surface (in a vacuum) the vertical descend of an object will be constantly accelerated at an average rate of 9.8 m/s2
- The value 9.8 m/s2 is referred to as the acceleration due to gravity or the gravitational field strength of the Earth.
- The size of a planet will determine the value of g around its surface. On the Moon gmoon is 1/6 of the value of gEarth.
-
g is a vector and as such it has magnitude and direction. Therefore g = -9.8 m/s2 or
g = 9.8 m/s2 [down] because its vector direction is down (pointing towards the center of the Earth.). - An object thrown up it the air will have positive but decreasing initial velocity. And negative but increasing final velocity.
- An object in free fall (in air) will not continue to accelerate indefinitely. Depending on its size and cross sectional area an object will reach a point where it will stop accelerating due to air resistance. After this point it will continue to fall at a constant rate called TERMINAL VELOCITY.
- The terminal velocity of an averaged size human is about 55 m/s.
- The acceleration and the velocity of an object are not always in the same direction
- An object thrown up in the air will reach zero velocity at its highest point of travel but the acceleration will never be zero
Example:
A golf ball dropped down from a cliff at the exact same time as a second ball (exactly the same as the first) is shot up in the air will meet the the second ball at point y in the air. At what time will they meet?
Solution:
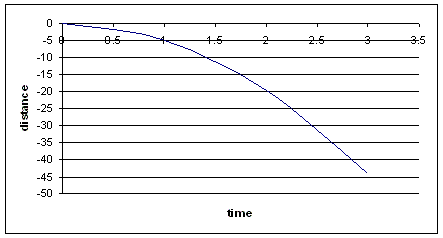
Set up a co-ordinate axis at the top of the cliff. Now the distance travelled by the first ball on its way down can be described by the following graph assuming it is starting from rest.
Graph of an object in Free Fall falling from rest from a height h