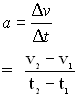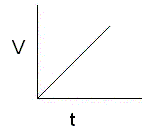Graphical Analysis of Linear Motion
A. Uniform Motion - Constant Speed - no acceleration

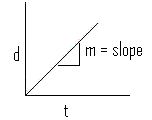
The slope m of the position-time graph gives the velocity of the object even when the relation between the position (d) and the time (t) is not a straight line..
We note that "m", the slope of the line (of the form, y = mx + b) is constant and can be calculated by several methods.
1. Slope = rise/run
2. 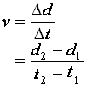
B. Uniformly Accelerated Motion - Variable Speed
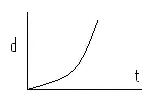
We know that the velocity is changing as time goes on because the slope of this line is not constant and the function (of the form y = ax2 + bx + c) is an increasing function.
To analyze this function properly one would need to take the first derivative of the function using Calculus.
It is sufficient to say, however that we can still obtain some useful information by relying on graphical analysis techniques.
1. Average velocity
To obtain the average velocity between two points in time (say t1 and t2) we can draw the secant line between these two points and calculate the slope of the secant line.
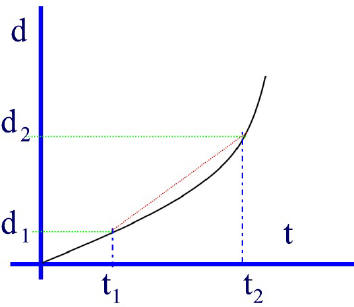
The slope of the secant line (the line that cuts the curve at the two intersecting points (d1,t1 and d2, t2) can be calculated by the usual slope method:
slope (of secant line) = Delta d / Delta t
This gives us the average velocity between the time interval from t1 -to- t2
Therefore: vav = v = slope or,
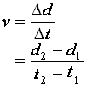
2. Instantaneous Velocity
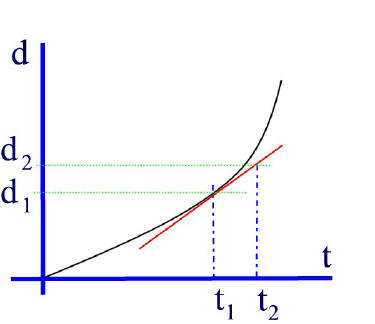
To obtain the instantaneous velocity, that is, the velocity at one instant (one point in time -- say at exactly t1), one must take the slope of the tangent line that just touches the curve at that point.
i.e. Vinst = slope of tangent
Vinst = v or, using the slope equation we calulte the slope of the tangent (the red line):
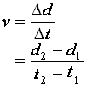
C. Acceleration
1. Non-uniform Acceleration
Using a method similar to deriving velocity from distance-time graphs, we can obtain values of acceleration from velocity-time graphs.
The slope of the tangent to a v-t graph at one point in time will give instantaneous acceleration [ainst] in the case where there is non uniform (changing) acceleration.
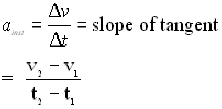
2. Uniform Acceleration
If the acceleration is constant the v-t graph will be a straight line.
The slope of this line will give us the acceleration.