Projectile Motion
Projectile motion is the motion of an object launched or propelled at an angle 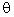 with respect to the horizontal
with respect to the horizontal
The standard equations describing the motion of an object in two dimensions can be applied to this special case of accelerated motion which occurs, in the vertical direction, under the influence of the acceleration due to gravity.
This is also a case of non-accelerated motion (only) in the horizontal direction.
The animation below describes the properties of a typical example of a projectile along its path of motion (known as the trajectory).
-
The projectile angle is
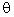
-
The initial velocity V1 is tangent to the path of motion at an angle
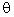 with respect to the horizontal therefore, it has horizontal and vertical components.
with respect to the horizontal therefore, it has horizontal and vertical components. -
The horizontal component of the initial velocity is called V1x; where V1x = V1 (cos
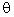 )
)
![]() Review vector addition using components for a better understanding of this topic
Review vector addition using components for a better understanding of this topic
-
The vertical component of the initial velocity is called V1y; where V1y = V1 (sin
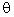 )
) - The trajectory (the path of the projectile) is a parabola. The parabola is symmetrical about a point half way between the origin and the total horizontal distance traveled by the projectile.
- At the half time point (t1/2), the projectile reaches its maximum height.
- The total horizontal distance (from the origin to where the projectile lands) is called the range (R). This is the total distance traveled by the projectile (horizontally) in the x-direction
- When the projectile lands at time t (the total flight time), its vertical distance is zero (ground level)
- A projectile path (because it is a parabolic trajectory) will have two roots
- Projectiles can be analyzed as a function [y = f(t)] of time t, and as a function of horizontal distance x [y = (fx)]
Important Physics principles of projectiles:
- The horizontal velocity Vx, is always constant -- not affected by gravity (i.e. ax = 0)
- The vertical velocity Vy, is affected by gravity -- it is positive but decreasing for the first part of the trajectory and negative but increasing for the second part of the trajectory. (i.e. ay = -9.8 m/s2).
- At the top of its flight (at t1/2), the slope of the tangent to this parabola is zero, therefore the vertical velocity Vy at that point is zero.
-
A projectile launched at angle
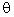 and an object dropped at the same time from the same height, will reach the ground at the same time. See illustration below.
and an object dropped at the same time from the same height, will reach the ground at the same time. See illustration below.
Equations of motion relating to projectiles
![]() Note the hints below each equation. These are given so that you can identify the correct conditions to use each equation in solving problems.
Note the hints below each equation. These are given so that you can identify the correct conditions to use each equation in solving problems.
| Projectile Motion equations and Linear Motion Equations | ||
| Linear Equations of Motion | Projectile Motion Analysis | |
| Horizontal | Vertical | |
V2 = V1 + a 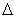 t t |
The horizontal velocity of a projectile is always constant |
V2y = V1y+ 2g 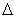 t t |
V22 = V12 + 2 a  d d |
V2y2 = V1y2 + 2g y | |
 d = V1 d = V1 t + 1/2 at2 t + 1/2 at2 d = Vav d = Vav 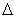 t t(use in non-accelerated motion conditions only) |
The horizontal distance is calculated by: x = V1 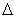 t tThe Range (R) is the maximum horizontal distance:
R = V12 (sin 2 |
The Height (h) can be calculated by: This equation can also be rearranged to solve for time - use the quadratic formula to get the final answer. |
| Vav = (V1 + V2) / 2 | To find the total time use y = 0 |
Maximum Height can be also be found by using 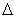 t = t1/2 t = t1/2 |
|
Use in free fall to calculate height:
|
V1x = V1 (cos 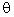 ) )This gives you the initial horizontal velocity |
V1y = V1 (sin 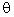 ) )This gives you the initial vertical velocity |
|
This gives you the instantaneous velocity at any point along the trajectory of the projectile |
||
|
Substitute the acceleration a with g (where g = - 9.8 m/s2) when dealing with free fall or projectiles. |
||
![]() Try some of Galileo's famous experiments with falling objects. http://www.pbs.org/wgbh/nova/physics/galileo-experiments.html
Try some of Galileo's famous experiments with falling objects. http://www.pbs.org/wgbh/nova/physics/galileo-experiments.html
![]() Now try this problem:
Now try this problem:
In a monster truck show ( use this YouTube video for reference https://www.youtube.com/watch?v=uLbBx_25y3U ), a truck is set to “jump” over several cars lined up side-by-side by racing up a ramp inclined at 180 to the horizontal at a speed of 40 m/s. A ramp is setup on the other side of the cars, also inclined at 180. If each car is 2.5 m wide, how many cars can the truck realistically jump over?



