Waves & Pulses
A wave is a disturbance in a medium that transfers energy. These "disturbances" can be analyzed as Simple Harmonic Motion.
The smallest part of a wave, acting on one single particle of a medium is called a pulse. The sum of all pulses make up the wave pattern.
Here is an example of a transverse pulse. Here you will see the particle being displaced perpendicularly to the direction of travel of the pulse.
There are three main types of waves:
- Longitudinal
- Transverse
- Surface
In longitudinal waves the particles of the medium move perpendicularly to the motion of the wave.
Example: sound is a longitudinal wave
In transverse waves the particles of the medium move parallel to the motion of the wave.
Example: a guitar string vibrating when struck
In surface waves the particles of the medium move in circular patterns relative to the motion of the wave
Example: water waves created by a rock dropped in a pond
![]() External resources: http://www.acs.psu.edu/drussell/demos/waves/wavemotion.html
External resources: http://www.acs.psu.edu/drussell/demos/waves/wavemotion.html
Period, Frequency, and Amplitude
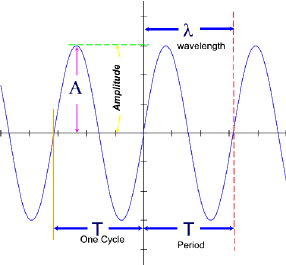
Properties of a Wave
Refer to the above diagram
Amplitude: The maximum displacement (measured in linear units --meters, centimeters, nanometers, etc.) of the particles of a medium due to the action of a wave or pulse or other harmonic disturbance.
Period: The time it takes a wave to complete one entire cycle. The symbol for period is “T”. The unit for period is the second (s).
Frequency: The number of repeated actions per unit time. When we talk about the frequency of a wave we define frequency as the number of cycles per unit time. The symbol of frequency is “f”. The unit of frequency is the cycle/second or the Hertz [Hz].
The relationship between frequency and period is that Period is the reciprocal (or the inverse) of frequency and vice versa.
In mathematical symbols:
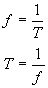
The Universal Wave Equation:
The universal wave equation tells us that the speed of a wave depends on its frequency and its wavelength. This equation can be derived from simple equations of motion.
- Recall that V = d/t (total distance/total time).
- Consider one full cycle of a wave or one wavelength. The total time elapsed in this cycle is the period of the wave (T) and
- Recall that T = 1/f
- The total distance traveled in one cycle is in fact the wavelength l.
Now, substituting these symbols in the equation v = d/t we obtain
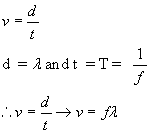
The equation
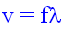
is known as the Universal Wave Equation because it applies "universally" to all types of waves traveling in any medium.


