Free Fall:
Free Fall is defined as the state of vertical (downward) motion of an object occurring solely under the influence of gravity. The object will have no strings attached to it, no self propelling engines or fuel sources, no other machines, pulleys, etc. governing its descend.
A rock falling off a cliff is said to be in "free fall"
Gravitational Field Intensity
What causes "free fall"? Think of the Earth as a giant magnet that attracts everything towards its center.
This attraction is due to a "force field" that surrounds the Earth; much like the area surrounding a magnet.
![]() This is known in Physics as the "Force-at-a-distance" effect. Unlike, for example, the force experienced by a soccer ball when you kick it - here you have to apply an actual "contact force" to make the ball change its state of motion.
This is known in Physics as the "Force-at-a-distance" effect. Unlike, for example, the force experienced by a soccer ball when you kick it - here you have to apply an actual "contact force" to make the ball change its state of motion.
We will revisit this concept when we review Newton's Laws of Motion.
The force field due to gravity surrounding a planet (gravitational field intensity) is pretty well constant around the surface of the planet.
The magnitude (or value, or size) of the gravitational field intensity on earth is a constant called g. We will discover the value of this constant with a simple experiment.
Let us recall two basic terms before we start or little experiment.
- mass - a scalar quantity - the amount of substance in an object - measured with a scale or balance in kg, the symbol for mass is m
- Force of gravity - a vector quantity.
In everyday language the mass of an object is often referred to as the "WEIGHT" of the object. Actually, the weight of an object, scientifically speaking, is the tforce of attraction with which an object falls down to Earth. Weight is measured with a spring scale in N (Newtons) and we prefer to call iot Force of Gravity. The symbol for force of gravity is Fg
Procedure: Using a digital scale and a spring balance we will measure the mass of a red apple and its force of gravity repspectively. Then we wiill do the same with a green apple.
Refer to the images below
Step 1. Let's measure the mass (m) of two apples with a balance and then their respective forces of gravity (Fg) with a spring scale
| Object | Mass (m) | Force of Gravity (Fg) | |
| grams | kilograms | Newtons | |
| Red Apple |  |
0.256 kg |  2.50 N 2.50 N |
| Green Apple |  |
0.136 kg |  1.40 N 1.40 N |
Step 2. We organize the data in a table
| object | mass ( kg) | Force of Gravity (N) |
| m | Fg | |
| red apple | 0.256 | 2.50 |
| green apple | 0.136 | 1.40 |
Step 3. We plot the data collected in the table above (recall that mass (m) should be on the x-axis because it is the independent variable) and we draw the line of best fit. See graph below:
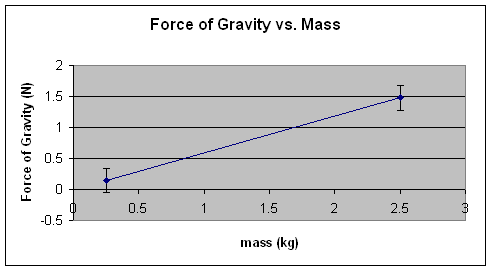
Step 4. We calculate the slope of the line
![]() Note that m vs. Fg is a straight line - We say that there is a linear relationship between Force of Gravity and Mass
Note that m vs. Fg is a straight line - We say that there is a linear relationship between Force of Gravity and Mass
![]() Note that this graph is a straight line of the form y = kx, (where k is the slope of the line)
Note that this graph is a straight line of the form y = kx, (where k is the slope of the line)
Because this is a linear relationship we can arrive at a simple equation that relates the force of gravity Fg to the mass m. This simple equation is:
Fg = k m
k is the slope of the line. We can calculate it very quickly from the graph using slope = Rise/Run, where the slope is the constant k in this case
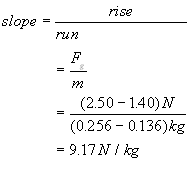
The value of the slope of this graph is 9.7 N/kg
Step 5. Let's test this value against a controlled value. A controlled value is a value that we can rely on for accuracy.
To do this we take the mass and weight of a 200 g standard mass
 |
 |
|
Here we have a 200 g mass or 0.200 kg |
Here we have the corresponding weight or force of gravity of almost 2.0 N |
Analysis:
- From the slope of the line in the graph above we see that the relationship between mass and force of gravity is linear
- The slope of the line yields a constant value of about 10 N/Kg - taking into account accuracy and sources of error
- The controlled value for a similar relationship is in fact 10N/kg
Inferences:
Any object (regardless of its mass) experience a force of gravity nearly 10 times the value of its mass.
This is due to a constant gravitational field intensity (or acceleration due to gravity) around the surface of the Earth.
The accepted or lab-tested value of this constant is 9.81 N/kg or 9.81 m/s2.
Conclusion:
The gravitational field intensity near the surface of the Earth is 9.81 N/kg or 9.81 m/s2
The symbol for this quantity is small g  g = 9.81 N/kg or 9.81 m/s2
g = 9.81 N/kg or 9.81 m/s2
![]() Note that the units for g can be expressed as either N/kg or m/s2
Note that the units for g can be expressed as either N/kg or m/s2


