Parent Category: Physics 11-U

Lab: Confirm that Newton's Law of Universal Gravitation  is an inverse square law

Gravit1 (1)

Given: the following data 

Average Earth -Moon Distance
 (m)		 Radius of Moon
(m)		 Radius of Earth
(m)		 Mass of Earth
(kg)		 Mass of Moon
(kg)		 Mass of Sun
(kg)		 Average Earth -Sun Distance
 (m)		 Radius of the Sun
(m)
3.84 x 10 6 1.74 x 106 6.38 x 106 5.98 x 1024 7.35 x 1022 1.99 X 10 30 1.496 x 10 11 6.96 x 108
               

 

Task: use graphical techniques to confirm that  Newton's Law of Universal Gravitation  is an inverse square law.

Solution:

noteNote: The center-to-center distance between the Moon and the Earth is the distance between the two celestial bodies plus their respective radii.  i.e.  

Gathering and Compiling additional Information:

For The Moon -Earth System 

R1 = 1.74 x 106 m + 6.38 x 106  m + 3.84 x 10 6 m  = 1.196 x 10 7 m      

For the Sun -Earth System

R2 = 1.496 x 1011 m + 6.38 x 106  m + 6.96 x 10 8 m  = 1.50 x 10 11 m

Procedure:

Use the Equation for the Law of Universal Gravitation Gravit1 (1)

  1. Find the forces for Moon -Earth System
     F1 = 2.05 x 1023 N
  2. Find the forces for the Sun -Earth System
    F2 = 3.53 x 1022 N
  3. Compile the data in a chart and Plot the data on a graph
System Forces (N) Distances (R)
(m)		 Distances-squared (R)2 , (m2) Product of Masses
(kg2)
Earth-Moon 2.05 x 1037 1.196 x 10 7 1.430 x 10 14 4.57 x 1047
         
Earth-Sun 3.53 x 1022 1.50 x 10 11 2.25  x 10 22 1.19 x 1055
         

 

noteHere is the same data and its analysis using spreadsheets

System Forces (N) Distances (R) Distances-squared (R)2 , (m2) Product of Masses Inverse Distances-squared (1/R)2 , (1/m2)
(m) (kg2)
Earth-Moon 2.05E+37 1.20E+07 1.43E+14 4.57E+47 6.99E-15
Earth-Sun 3.53E+22 1.50E+11 2.25E+22 1.19E+55 4.44E-23

 

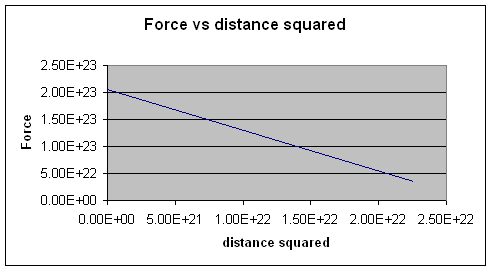
Univer7 

 This shows that in the relationship F α 1/R2,Force is inversely proportional to the distance squared

 

noteTo confirm the inverse square relationship we can plot F vs. 1/R2

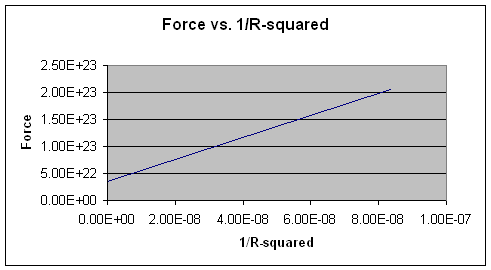
Univer8

 

noteNote: F vs. 1/R2 gives us  a linear relationship.  

 

Conclusion: the Law of Universal Gravitation is a an inverse square law