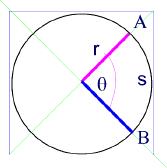
When the arc s = r , Ө = 1 radian measure, therefore Ө = s / r
Wher the angle Ө is measured in radians.
- Ө is known as the angular distance.
- s is the linear distance (generally called "d")
d = r Ө
Since Ө = s / r (or Ө = d / r), we can relate the linear distance d to the angular distance Ө using the simple equation:
Recall that
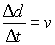
This can be obtained by dividing the left side of the above equation by ∆t).
Dividing the right side of the same equation by ∆t we obtain the following
.
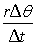The factor
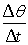
is known as the angular velocity.
The symbol for angular velocity is ω (pronounced "omega"). Its units are "radians per second -- rad/s".
Where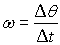 
and
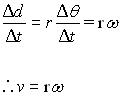
We can also express the angular velocity ω in terms of the frequency of rotation "f".
Starting from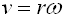 
we get...
Therefore: ω = 2πf
In this case f is measured in revolutions per second (Hz) and ω is measured in radians per second
Similarly we can show that by dividing both sides of the equation
.gif)
by
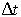
we can obtain expressions for acceleration.
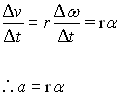
- The left side of the equation defines the linear acceleration "a".
- The right side of equation defines the angular acceleration "a" (pronounced "alpha").
Recall that in a full circle, the total radian/angular measure is θ = 3600
The linear distace around the circle, known as circumference, is d = 2 π r (the total circumference of the circle).
We measure θ in radians (a linear measure) instead of degrees.
If d = r θ, then 2πr = [3600] r or simply 2π [radians] = 3600 ,
Consequently the units of the acceleartion, a are m/s2 and the units of "a" are radians/s2 [rads/s2]
Comparing Angular equations of Motion to Linear Quantities |
| Linear Equations of Motion | Angular Equations of Motion |
| v2 = v1 + a t |
ω2= ω1 + a t |
| v22 = v12 + 2 a d |
ω22= ω12 + 2aӨ |
| d = v1t + 1/2 at2 |
Ө = ω1 t+ 1/2at2 |
| vav = (v1 + v2) / 2 |
ωav = (ω1 + ω2 ) / 2 |
|
d = r Ө |
|
|
ω = 2 π f |
