The Law of Universal Gravitation
The force of attraction F between two objects with respective masses m1 and m2 separated by a center-to-center distance R, anywhere in the universe, is described by Newton's Law of Universal Gravitation:
The two postulates of this law are:
-
The force of attraction is directly proportional to the product of the objects' masses
-
The force of attraction is inversely proportional to the distance (taken from their respective centers) squared
If we combine the above statements mathematically, we obtain the following relation:
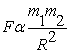
![]() This relationship is known as an inverse-square law. This means that one factor (F) is inversely proportional to another factor (R) squared
This relationship is known as an inverse-square law. This means that one factor (F) is inversely proportional to another factor (R) squared
We translate the above relationship into a definite equation by removing the "proportionalty symbol" ( ) and replacing it with the "equal sign" (=) and a constant. The symbol for this constant is "G"
) and replacing it with the "equal sign" (=) and a constant. The symbol for this constant is "G"
Therefore:
.gif)
Where:
- F is the force of attraction between two masses m1 and m2 anywhere in the Universe, and
- and, G is the Universal Gravitational Constant: G = 6.67 X 10-11 Nm2 /Kg2
![]() The animation below is a very simple illustration of the inverse-law law
The animation below is a very simple illustration of the inverse-law law
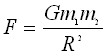
![]() Notes: When you use the above equation
Notes: When you use the above equation
- Observe proper units (mass in kg, distance in m, Force in [N]
- The distance R has to be center-to center; i.e. from the center of one mass to the center of the other
- Don't forget to square the distance R
- Remember the significance of the Inverse Square Law


