Addition of Vectors using the components method
When adding two or more vectors using the components method follow these guidelines.
- Sketch the vectors on a piece of paper. This will give you an idea of their relative positions and magnitudes.
- Calculate each vector's horizontal (x) and vertical component (y) using trigonometry
- add all the horizontal components together (taking into account the sign of each vector component)
- add all the vertical components together (taking into account the sign o feach vector component)
- Now you have a resultant horizontal vector in the x direction and a resultant vertical vector in the y direction.
- Use the resultant x and y vectors to calculate the total resultant vector.
- Calculate the angle and state the direction of the final (resultant) vector.
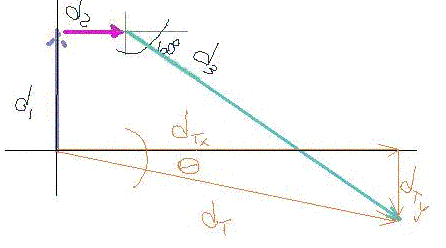
This animation illustrates that, irrespective of the path, from the initial position (the tail of first vector) to the final position (the head of last vector), the resultant vector VTot will have only two components: an x (horizontal) component and a y (vertical) component. Here the vectors a, b, and c each have their individual x and y components which, when added together to all the x and y components respectively, will give a total horizontal component V1x and a total vertical component V2y.
Example:
Find the final displacement of a man who first walks North for 5.0 km, then East for 3.0 km and finally [E600S] for 8.0 km.
Given: d1 = 5.0 km [N], d2 = 3.0 km [E], d3 = 8.0 km [E600S]
Find:
- All components
- dtx
- dty
- dt
-
 (the direction of the final displacement vector dt)
(the direction of the final displacement vector dt)
![]() Here is a step-by-step method to approach the solution of problems involving the addition of vectors using the components method.
Here is a step-by-step method to approach the solution of problems involving the addition of vectors using the components method.
- Draw a quick sketch to guide you through the solution (doesn't have to be to scale - this is not a graphical solution)
- Set-up a table for each vector where you can enter the x and y components of each.
| Identify each vector |
Draw a quick diagram for each vector for reference |
calculate the X-Component using trigonometry |
calculate the Y-Component using trigonometry |
| d1 = 5.0 km [N] | 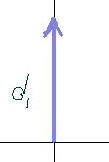 |
d1x = 0 | d1y = +5 |
| d2 = 3.0 km [E] | 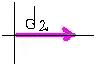 |
d2x = + 3 | d2y = 0 |
| d3 = 8.0 km [E600S] |  |
 |
 |
| Totals ( x and y components together) |
 |
dTx = 0 + 3 + 4 = +7 km [to the right] |
dTy = 5 + 0+ (-)6.9 = -1.9 km [down] |
3. Once we have the components for the resultant dTx and dTy we can find the direction using inverse trigonometric functions
![]() Recall from your trigonometry
Recall from your trigonometry
dTy/dTx = tan 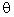
Therefore: 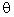 = inv tan (dTy/dTx)= 150
= inv tan (dTy/dTx)= 150
4. Use Pythagoras' Theorem to find the magnitude of total displacement :
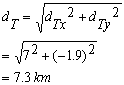
5. One final statement indicating the final answer with both magnitude and direction
The the man's total displacement is : 7.3 km [E150]