1. Non-Collinear Vectors
When vectors are in the same plane but are not acting along the same line of action they are known as non-collinear vectors.
Non collinear vectors can be added using three different methods:
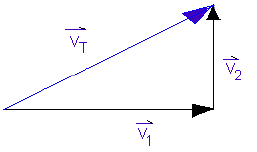
The general rule for adding vectors regardless of the method is still : "add vectors from tail to head". When two or more vectors are added together, the resulting vector is known as the "resultant".
![]() Note that in the illustration below the resultant VT is the sum of the vectors V1 and V2.
Note that in the illustration below the resultant VT is the sum of the vectors V1 and V2.![]() VT is drawn from the tail of the first vector (V1) to the head of the last vector (V2).
VT is drawn from the tail of the first vector (V1) to the head of the last vector (V2).
2. Direction of Vectors
Now let's say we place a resultant vector, d on a set of x-y coordinates with its tail at the origin (0,0). We want to find out its direction.
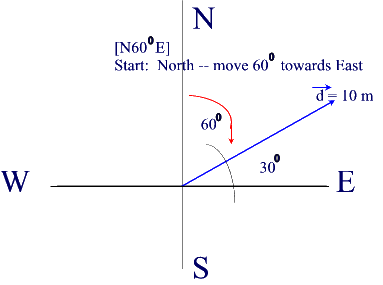
![]() Note that d is in a direction other that the standard North-South-East-West directions.
Note that d is in a direction other that the standard North-South-East-West directions.
![]() We use the the compass (or nautical directional system) to express its direction.
We use the the compass (or nautical directional system) to express its direction.
The diagram above demonstrates how to report the direction of a vector using a standard format.
This vector is found 600 East of North (or 300 North of East) and has a magnitude of 10 m. We can draw this vector using a protractor and a ruler.
Our starting point is the Y-axis and we move 600 from the North position towards the East position (the X-axis).
The standard notation to report the magnitude and direction of vector d is:
d = 10 m [N600E].
![]() Note: we can also say that d = 10 m [E300N].
Note: we can also say that d = 10 m [E300N].


