Chemistry 12

The de Broglie relation

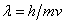                                is a key to the wave properties of small particles.

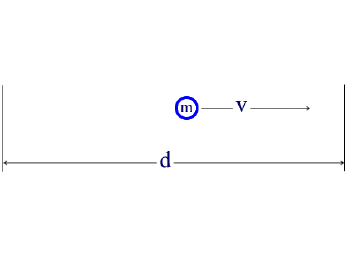
 The de Broglie relation states that there must be a wave associated with a particle of mass m moving at a speed v through a distance d, as shown in the diagram below. 

The wave must fit into the space allowed to the particle.

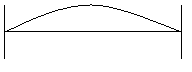
The wave can have finite amplitudes inside the boundaries of the system; the amplitudes at the walls must be zero.

a. n = 1, λ /2 = d

b. n = 2, 2λ =d

 c. n = 3, 3λ = d

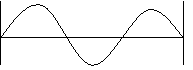
 The examples above show some waves that meet these conditions.

 Mathematical expressions called wave functions can be written which give the amplitude of each wave as a function of position. Accordingly, if the square of the value of the wave function at any given point is taken, this equals the probability of finding the particle at that point. Examining a wave function similar to that of figure “a” above, the particle would be found in the middle region and never near the wall.

For small particles it is not possible to define such properties as position and momentum definitively because these properties have associated probabilities. This is the Heisenberg uncertainty principle. This principle really says that the more accurately we know a particle’s position, the less accurately we can know its momentum, and visa versa. Applied to the electron, the uncertainty principle implies that we cannot know the exact motion of the electron as it moves around the nucleus. It is therefore not appropriate to assume that the electron is moving around the nucleus in a well defined orbit, as in the Bohr model.

 The wave function that describes the waves associated with a particle allows for the calculation of the energy of the particle. For waves that satisfy the condition that the amplitude be zero at the walls (see diagrams “a”, “b”, and “c” above), the wavelengths, λ, of the allowed waves can be set by the relationship

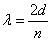
where

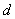
is the distance between the walls and

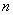
is an integer equal to 1, 2, 3, ….. 

By combining de Broglie’s equation with the equation above, an equation that imposes a quantum condition on the momentum,

 ,

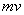of the particle is achieved.

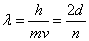
or rearranging

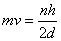
From your Physics you know that mv is the momemunt of a particle

But,  momentum can have only certain values, this limits the energy of the particle as decribed mathematically below:

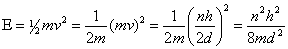
This equation tells us that a particle confined to move in a region of any length, will have certain energies allowed to it. 

Those energies depend, on the mass, ,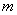

of the particle, the distance,

 ,

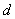through which it moves, and the quantum number,

Since = 1, 2, 3,…,

the particle can have different energy values;

the lowest being for 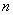=1.

Also, the lowest energy available depends on the mass and the interval length to which the particle is confined. From the equation you can see that the energy varies inversely with the mass. Every time the mass is decreased by a factor of two, the energy is doubled.

The minimum energy also varies inversely with the square of the length through which the particle can move. If the length is halved then the quadruples the energy of the particle.