BLACK BODY RADIATION
What is a black body?
A black body is a theoretical object that absorbs 100% of the radiation that hits it. Therefore it reflects no radiation and appears perfectly black. In practice no material has been found to absorb all incoming radiation, but carbon in its graphite form absorbs all but about 3%. It is also a perfect emitter of radiation. At a particular temperature the black body would emit the maximum amount of energy possible for that temperature. This value is known as the black body radiation. It would emit at every wavelength of light as it must be able to absorb every wavelength to be sure of absorbing all incoming radiation. The maximum wavelength emitted by a black body radiator is infinite. It also emits a definite amount of energy at each wavelength for a particular temperature, so standard black body radiation curves can be drawn for each temperature, showing the energy radiated at each wavelength.
Black Body Radiation Curves
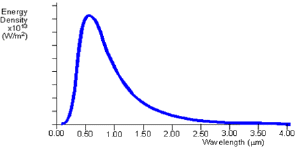
Fig 1: Theoretical black body curve for 5000K
The black body radiation curve (Fig1) shows that the black body does radiate energy at every wavelength. The curve gets infinitely close to the x-axis but never touches it. The curve touches at infinite wavelength. It also shows that the black body emits at a peak wavelength, at which most of the radiant energy is emitted. At 5000K the peak wavelength is about 5x10-7m (500nm) which is in the visible light region, in the yellow-green section. At each temperature the black body emits a standard amount of energy. This is represented by the area under the curve.
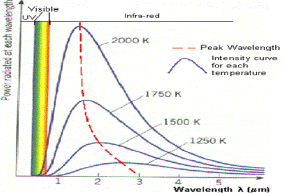

Fig 2: Black body radiation curves showing peak wavelengths at various temperatures
This graph shows how the black body radiation curves change at various temperatures. These all have their peak wavelengths in the infra-red part of the spectrum as they are at a lower temperature than the previous graph.
The graph shows:
1. As the temperature increases, the peak wavelength emitted by the black body decreases.
The graph shows:
1. As the temperature increases, the peak wavelength emitted by the black body decreases.
2. It therefore begins to move from the infra-red towards the visible part of the spectrum. Again, none of the graphs touch the x-axis so they emit at every wavelength.
This means that some visible radiation is emitted even at these lower temperatures and at any temperature above absolute zero, a black body will emit some visible light.
The graph also shows:
The graph also shows:
3. As temperature increases, the total energy emitted increases, because the total area under the curve increases.
4. It also shows that the relationship is not linear as the area does not increase in even steps. The rate of increase of area and therefore energy increases as temperature increases.
The failure of physics to account for the decrease in energy emitted at short wavelengths (the ultraviolet wavelengths) became known as the ultraviolet catastrophe.
Max Planck
A major breakthrough was made by Max Planck who made a formula that agreed with experimental data. However, he had major problems proving this law. His idea was that the oscillating electrons of the surface atoms of the black body emitted radiation according to Maxwell's laws of electromagnetism. Before Planck it was assumed that these could have any value of energy but Planck decided that the energy must go up in discrete amounts (quantized) because the frequencies of the oscillating electrons could only take certain values. As energy is proportional to frequency
E = hυ,
Where h is the Planck constant 6.626 x 10-34 Js
If frequency can only take discrete values, this means that energy is also quantized. The electrons have a fundamental frequency (like standing waves on a string) and the frequency can only go up in whole multiples of this frequency, called the quantum number. This assumption led Planck to correctly derive his formula.


