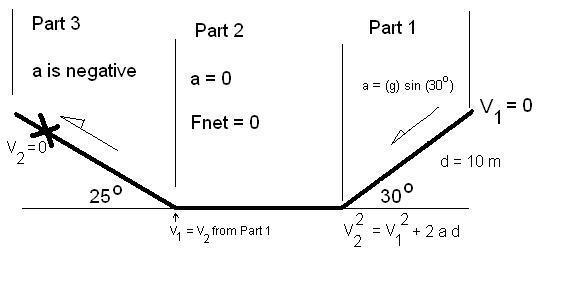
Forces on Inclined Planes:Problem:
Problem:
A skier goes down a smooth 30o hill (frictionless) for a distance of 10 m to the bottom of the hill where he then continues on a frozen, frictionless pond. After that, he goes up a hill inclined at 25o to the horizontal. How far up this second hill does he go before stopping if the coefficient of friction on this hill is 0.10?
Analysis and Solution:
Part I - Accelerated Motion
a = (g)(sin30o)
= 9.8 X 0.5 m/s2
V1 = 0 ( V2 ) 2 = ( V2 ) 1 + 2(a)(d) d = 10 m
( V2 ) = 9.9 m/s
Part II - No acceleration
No acceleation means a = 0, therefore, Fnet = ma = 0 and V1 is the same as V2 from Part 1.
Part III - Friction up an inclined plane

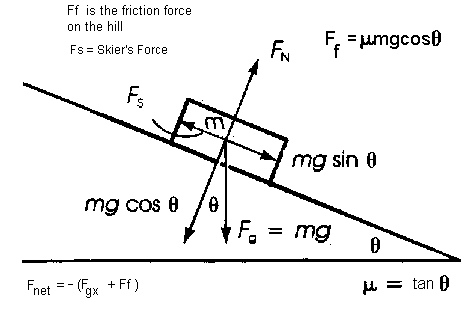
From the Free Body Diagram above
Fnet = -Fgx - Ff
ma = -(m)(g)(sin 25o) - µ(m)(g)(cos 25o)
m drops off on both sides of the equation
This is proof that the acceleration of an objevct sliding down an inclined plane is independent of the mass of the object.
What factors influence the acceleration of the object?
Hint: Look at the above equation.
we solve for the acceleration, a
a = - 4.99 m/s2
we use the formula below and the acceleration found above to find the distance, d
Where V2 is zero (that's when the skier stops)
Solving for d, where V1 = 9.9 m/s from part 1, and a = -4.99 m/s2
We obtain a value for d:
d = 9.8 m
Therefore the distance traveled by the skier before he stops up the second hill is 9.8 m