Acceleration is the rate at which speed increases or decreases. Acceleration involves a changes in speed or a change in velocity during a time interval. Acceleration can be both a scalar quantity and a vector quantity. It is a scalar quantity when we consider only its magnitude. If we also indicate the direction in which a moving object is accelerating, then we are defining acceleration as a vector quantity.
When an object slows down we say it is decelerating. Deceleration (many teachers don't like to use this term) is really negative acceleration. The symbol for acceleration is a . The units for acceleration are [m/s2 ] {"meters-per-second-squared"}.
![]()
"a" with no arrow on top = scalar acceleration; 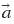 (with the arrow on top) = vector acceleration
(with the arrow on top) = vector acceleration
Acceleration over a definite time interval is known as average acceleration. Acceleration calculated at each instant (very small time segment) along the path of motion of a moving object is known as instantaneous acceleration.
The equation for average acceleration is :
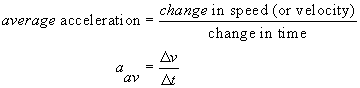
Note that  is the change in speed or velocity during the time interval (change in time)
is the change in speed or velocity during the time interval (change in time) 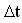 . This means that if at time t1 the speed of an object was v1, at a later time t2, its corresponding speed is v2.
. This means that if at time t1 the speed of an object was v1, at a later time t2, its corresponding speed is v2.
![]() [Tip: The symbol
[Tip: The symbol 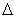 ("delta") is a mathematica operatpor that indicates "a Final quantity - an Initial quantity".
("delta") is a mathematica operatpor that indicates "a Final quantity - an Initial quantity".
![]()
[Your textbook or teacher may use the subscripts "i" for initial and "f"" for final ... this site uses "1" for initial and "2" for final]
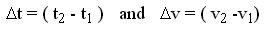
Example:
A police car is cruising at 50 km/h along a straight road. A motorist zooms past the cruiser. The police officer steps on the gas and catches up to the speeding car 30 s later at that instant her speedometer was reading 80 km/h.
What was the average acceleration of the police car during the 30 s?
Given: v1 = 50 km/h v2 = 80 km/h
let the initial time t 1 = 0 then, t 2 = 30s
Find: aav
Solution:
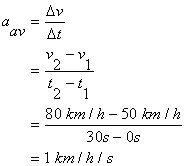
![]() The standard unit for acceleration is the m/s2 . Therefore we will convert our answer (
The standard unit for acceleration is the m/s2 . Therefore we will convert our answer (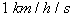 ) to m/s2 .
) to m/s2 .
1 km = 1000 m and 1 h = 3600 s Therefore:
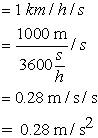
The police cruiser accelerated at 0.28 m/s2


