Mathematics

Horizontal & Vertical Components of Vectors

A vector in space (3-dimensional) can be defined by its x, y, and z coordinates.

Figure 1:
Point P in 2-D is defined by its Cartesian co-ordinates 
(x , y) with respect to the origin (0,0)

We will analyze vectors in two dimensions.

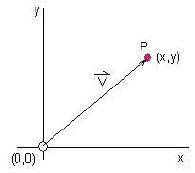
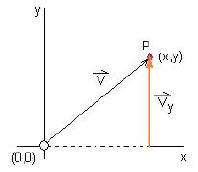
Figure2:
The vector V maps the point P in terms 
of its position from the origin

In a two dimensional frame we need only consider its x and y co-ordinates. 

Note: In figure 2, the tail of vector V is at the origin and its head ends at point P

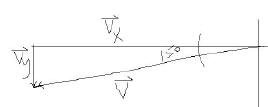
Any vector in 2-D can be expressed in terms of its resultant.  A resultant is obtained by adding a vector's vertical component in the y direction (see figure 3) to its horizontal component in the x direction (see figure 4) .

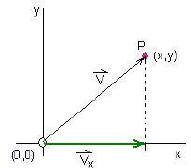
Figure 3:
V_y is the vertical component of the 
vector v 

Figure 4:
V_x  is the horizontal component of the 
vector v 

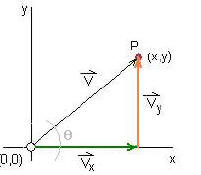
Figure 5 is a diagram showing both the x and y components defining vector v.  

Vecor V is the resultant vector when Vx is added to Vy from the tail of Vx to the head of Vy

Figure 5:
the x and y components of vector v

We can  define V_x and V_y in terms of  V and the angle 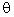 using trigonometry:

Know your basic trigonometry functions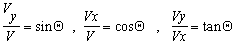 

Rearrange the first two equations to obtain expressions for Vy and Vx (the x and y components of vector v):

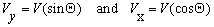
 The resultant vector v (see figure 5 above) will now be: v = v_x + v_y

Examples of problems involving vector components:

1. What are the horizontal and vertical components of an airplane moving at 300 km/h [E65⁰N]?

Refer to diagram below

 
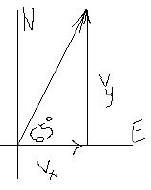
Here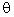 =  65 ⁰  and v = 300 km/h

Answer: Vx = 127 km [to the right] ; Vy = 272 km [up] 

Did you get the answer?  Click here to see the solution or hint

2. What are the components of a vector 8 cm long with bearings [W15⁰S]?

Answer: Vx =7.7 cm [to the left] ; Vy = 2.1 cm[down]

 Did you get the answer?  Click here to see the solution or hint